Robust neuromorphic coupled oscillators for adaptive pacemakers

Abstract

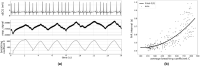
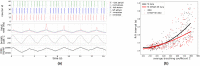
Neural coupled oscillators are a useful building block in numerous models and applications. They were analyzed extensively in theoretical studies and more recently in biologically realistic simulations of spiking neural networks. The advent of mixed-signal analog/digital neuromorphic electronic circuits provides new means for implementing neural coupled oscillators on compact, low-power, spiking neural network hardware platforms. However, their implementation on this noisy, low-precision and inhomogeneous computing substrate raises new challenges with regards to stability and controllability. In this work, we present a robust, spiking neural network model of neural coupled oscillators and validate it with an implementation on a mixed-signal neuromorphic processor. We demonstrate its robustness showing how to reliably control and modulate the oscillator's frequency and phase shift, despite the variability of the silicon synapse and neuron properties. We show how this ultra-low power neural processing system can be used to build an adaptive cardiac pacemaker modulating the heart rate with respect to the respiration phases and compare it with surface ECG and respiratory signal recordings from dogs at rest. The implementation of our model in neuromorphic electronic hardware shows its robustness on a highly variable substrate and extends the toolbox for applications requiring rhythmic outputs such as pacemakers.

Figure 1

Spiking neural network architecture for implementation on neuromorphic processor (a) We implemented our model on the mixed-signal spiking neural network processor DYNAP-SE which consists of four cores with 256 neurons each. (b) Example membrane trace of one neuron on the DYNAP-SE board. The neuron spikes at around t = 200 ms and receives several incoming spikes which are not sufficient to trigger an event. (c) Variability of synaptic time constants on one core of DYNAP-SE board due to device mismatch (n = 256). (d) A neuronal oscillator is the basic building block in our model. It consists of two reciprocally connected inhibitory and excitatory neuron populations. (e) In the complete model we use three neuronal oscillators to model the activation times of the right atrium, the left atrium and the combined ventricles. Additionally, we provide external feedback input (respiratory feedback) using the on-board FPGA on the DYNAP-SE board to modulate the heart rate modelling respiratory sinus arrhythmia. (f) To tune the model parameters we developed a structured tuning process based on a set of relations between the network function (oscillation properties) and the network parameters and structure. Here we illustrate the relation between the network parameters and the oscillation frequency of a single neuronal oscillator. The connection in bold is used to increase or decrease the speed of a single neuronal oscillator in the respective section of the phase diagram. (E: activity level of excitatory population; I: activity level of inhibitory population; yellow star: reference point to determine phase shift between oscillators).

Figure 2

Presence of RSA in sECG and respiratory signal recordings of dogs at rest (a) The first row shows the sECG recording and the second row the simultaneously recorded respiratory signal trace. An increase in the respiratory signal value corresponds to exhalation and a decrease corresponds to inhalation. In this recording, RSA is clearly visible in the continuous decrease in the dog’s heart rate over the course of the exhalation. The third row shows the instantaneous breathing coefficient C during the same period of time. The breathing coefficient C is introduced as a new variable to quantify the effect of RSA and can be understood as removal of the linear drift from the respiratory signal trace. (b) We quantify the presence of RSA based on the relation between the average breathing coefficient and the R–R interval. The plot shows the R–R interval durations plotted against the average breathing coefficient in the corresponding R–R interval. Every point corresponds to one interval extracted from our recordings of a healthy dog at rest. The plot shows that a longer R–R interval corresponds to a larger average breathing coefficient. The solid line corresponds to a second degree polynomial function G(C) which is fitted on the retrieved data points.

Figure 3

Cardiac pacemaker implementation with constant heart rate (a) The raster plot shows the events of all neurons of the three coupled neuronal oscillators on the DYNAP-SE board over 5 s. The inhibitory and excitatory populations of each oscillator are presented in different colors. The events are converted into activity traces (below) for each population. Here we only show them for the three excitatory populations. The stimulation time of each heart chamber is defined as the time point when the activity traces of the respective excitatory population crosses a predetermined and fixed threshold value. (b) After the initial iterative tuning process, we are able to set the system’s oscillation frequency explicitly by fitting a mapping function. The x-axis shows the desired oscillation frequency, the y-axis shows the oscillation frequency measured on the DYNAP-SE board after setting the biases based on the fitted mapping function. This plot shows that we are able to explicitly set the oscillation period of the coupled system to any value between 200 and 700 ms. (c) The delay (phase shift) between the activation of the heart chambers smoothly adjusts itself to the explicitly set heart rate without any further tuning.

Figure 4

Adaptive cardiac pacemaker implementation with respiratory feedback (a) We tested our implementation of an adaptive cardiac pacemaker on the DYNAP-SE board by providing real respiratory feedback signals. The last row shows an example trace of the raw respiratory signal recording over 16 s. The rows above show the corresponding breathing coefficient trace C(t) and the resulting input spike frequencies which define the strength of the inhibitory input modelling the respiratory feedback. The top row shows the system’s behaviour while receiving the respiratory feedback. Qualitatively, this shows a continuous decrease of the heart rate during exhalation and an increase during inhalation modelling the effect of RSA. (b) To evaluate our model more quantitatively, we extract the relation between every R–R interval and the breathing coefficient averaged over the period between the two respective R-peaks. The plot shows that our model reproduces the same relation that is also observed in physiological recordings.