Informing power and sample size calculations when using inverse probability of treatment weighting using the propensity score

Abstract

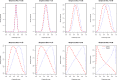
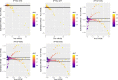
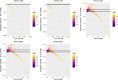
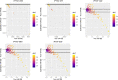
Propensity score weighting is increasingly being used in observational studies to estimate the effects of treatments. The use of such weights induces a within-person homogeneity in outcomes that must be accounted for when estimating the variance of the estimated treatment effect. Knowledge of the variance inflation factor (VIF), which describes the extent to which the effective sample size has been reduced by weighting, allows for conducting sample size and power calculations for observational studies that use propensity score weighting. However, estimation of the VIF requires knowledge of the weights, which are only known once the study has been conducted. We describe methods to estimate the VIF based on two characteristics of the observational study: the anticipated prevalence of treatment and the anticipated c-statistic of the propensity score model. We considered five different sets of weights: those for estimating the average treatment effect (ATE), the average treated effect in the treated (ATT), and three recently described sets of weights: overlap weights, matching weights, and entropy weights. The VIF was substantially smaller for the latter three sets of weights than for the first two sets of weights. Once the VIF has been estimated during the design phase of the study, sample size and power calculations can be done using calculations appropriate for a randomized controlled trial with similar prevalence of treatment and similar outcome variable, and then multiplying the requisite sample size by the estimated VIF. Implementation of these methods allows for improving the design and reporting of observational studies that use propensity score weighting.

Keywords: inverse probability of treatment weighting; power; propensity score; sample size; study design.

FIGURE 1

Distribution of the propensity score in treated and control subjects (primary simulations) [Colour figure can be viewed at wileyonlinelibrary.com]

FIGURE 2

Variance inflation factors/design effects for main simulations [Colour figure can be viewed at wileyonlinelibrary.com]

FIGURE 3

Comparing estimated and true variance inflation factor/design effect: normal distribution [Colour figure can be viewed at wileyonlinelibrary.com]

FIGURE 4

Comparing estimated and true VIF/DE: Beta distribution [Colour figure can be viewed at wileyonlinelibrary.com]

FIGURE 5

Comparing estimated and true VIF/DE: Chi‐squared distribution [Colour figure can be viewed at wileyonlinelibrary.com]

FIGURE 6

Comparing estimated and true VIF/DE: log‐normal distribution [Colour figure can be viewed at wileyonlinelibrary.com]