Tractography in Curvilinear Coordinates

Abstract

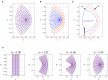
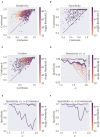
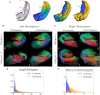
Coordinate invariance of physical laws is central in physics, it grants us the freedom to express observations in coordinate systems that provide computational convenience. In the context of medical imaging there are numerous examples where departing from Cartesian to curvilinear coordinates leads to ease of visualization and simplicity, such as spherical coordinates in the brain's cortex, or universal ventricular coordinates in the heart. In this work we introduce tools that enhance the use of existing diffusion tractography approaches to utilize arbitrary coordinates. To test our method we perform simulations that gauge tractography performance by calculating the specificity and sensitivity of tracts generated from curvilinear coordinates in comparison with those generated from Cartesian coordinates, and we find that curvilinear coordinates generally show improved sensitivity and specificity compared to Cartesian. Also, as an application of our method, we show how harmonic coordinates can be used to enhance tractography for the hippocampus.

Keywords: MRI; curvilinear coordinates; diffusion MRI; hippocampus; tractography.

Figure 1

This figure summarizes aspects of our simulation strategy. In (A), we have an illustration of the conformal coordinate system grid generated by Equation (3) with w = 1.99. In (B), we have the fibres, blue for tangential and red for radial, used to generate the diffusion signal. Notice that there is an overlap between the two tracts to depict the mixing of the signal from the two compartments, the opacity of the line is calculated from Equation (4). The orange dashed line is u_1/2. In (C), the region U_Σ, is the seeding area, the region U_T is the ground truth area occupied by the tangential tracts, and U_R is used to detect tracts that falsely traverse into the radial fibres. Notice that U_R is half of the region occupied by the radial tracts, this is done to reduce errors introduced by discretization. Also note that U_R is asymmetric, this choice is to reject false positives caused by purely radial tracts emanating from U_Σ, the focus is intended to be on the bent area. In (D), we show the effect of changing the parameter w on the curvature of the geometry.

Figure 2

This figure summarizes the sensitivity and specificity measurements from the simulations. In (A–C), the y-axis represents quantities calculated with using conformal coordinates and the x-axis represents quantities calculated with using Cartesian coordinates. The results from the whole parameter space are shown, the color of the markers represents the angle threshold, where the orange is low angles and purple is high. The size of the markers depicts the resolution, small markers are high resolution (smaller voxels) and larger markers are low resolution (larger voxels). In (A), for e.g., we see that we have high sensitivity for both Cartesian and conformal coordinates when using high resolution (small markers in the top right). In (D–F) we isolate the effect of the angle threshold and curvature, w, by fixing the resolution to its maximum value. In (D) we see the sensitivity, for both conformal and Cartesian coordinates (labeled), as a function of the angle threshold (color) and w (x-axis). In (E), we have analogous curves but for specificity when using Cartesian coordinates, and (F) is specificity when using conformal coordinates. In (E) the curves for all angles overlap except for 80° (minute deviation from angles < 80°) and for 90°. In (F) all curves overlap except for the 90° one.

Figure 3

This figure shows the tracts generated from the simulations. For brevity we divide the resolution (y-axis) and curvature (x-axis) parameter space into low, medium and high values giving nine tiles. The values for the resolution are 0.2, 0.7, and 1.2 mm, respectively, and the values for the curvature are 1.24, 1.66, and 1.99, respectively. In each tile the left image is generated from using Cartesian coordinates and right one is from using conformal coordinates. The colors of the tracts represent the angle threshold used. The blue outline shows the tangential region and the red shows the radial region. Since the high angle threshold (purple) tracts occupy the most area they are plotted first and the lowest angle threshold tracts (orange) are plotted last.

Figure 4

In (A), we see the boundary conditions and the harmonic coordinates for the hippocampus. For example, to solve for coordinate u, U₀ is the source and U₁ is the sink, and Neumann boundary conditions are used for the rest of the hippocampus. An analogous procedure is used to compute the remaining coordinates. In (B) we see tracts in a coronal slice for the hippocampus of two subjects in the left hemisphere. The first column shows tracts generated from using Cartesian coordinates and the second column shows tracts generated from using curvilinear coordinates, (C) is analogous but for the right hemisphere. The seeds in both coordinate systems are identical. In (B,C), green represents the anterior to posterior direction, red represents right to left, and blue represents inferior to superior. In (D), we see a histogram for the normalized length distribution for the tracts, overlaid for each hippocampus, here blue is for Cartesian coordinates and orange is for harmonic coordinates, (E) is similar to (D) but for the mean curvature of the tracts.