Dissecting (un)crowding
- PMID: 34515740
- PMCID: PMC8444456
- DOI: 10.1167/jov.21.10.10
Dissecting (un)crowding
Abstract
In crowding, perception of a target deteriorates in the presence of nearby flankers. Surprisingly, perception can be rescued from crowding if additional flankers are added (uncrowding). Uncrowding is a major challenge for all classic models of crowding and vision in general, because the global configuration of the entire stimulus is crucial. However, it is unclear which characteristics of the configuration impact (un)crowding. Here, we systematically dissected flanker configurations and showed that (un)crowding cannot be easily explained by the effects of the sub-parts or low-level features of the stimulus configuration. Our modeling results suggest that (un)crowding requires global processing. These results are well in line with previous studies showing the importance of global aspects in crowding.
Figures



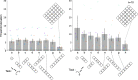
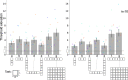

References
-
- Attneave, F., & Olson, R. K. (1967). Discriminability of stimuli varying in physical and retinal orientation. Journal of Experimental Psychology, 74(2p1), 149.
-
- Bach, M. (1996). The Freiburg Visual Acuity Test—Automatic Measurement of Visual Acuity. Optometry and Vision Science, 73(1), 49–53. - PubMed
-
- Ball, K., & Sekuler, R. (1982). A specific and enduring improvement in visual motion discrimination. Science, 218(4573), 697–698. - PubMed
Publication types
MeSH terms
LinkOut - more resources
Full Text Sources

