Geometry of gene regulatory dynamics
- PMID: 34518231
- PMCID: PMC8463785
- DOI: 10.1073/pnas.2109729118
Geometry of gene regulatory dynamics
Abstract
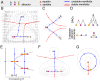
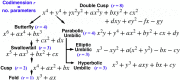
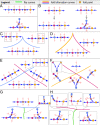
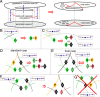
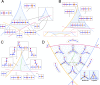
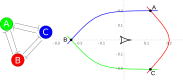
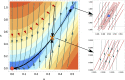
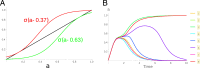
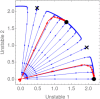
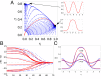
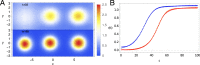
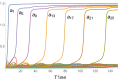
Embryonic development leads to the reproducible and ordered appearance of complexity from egg to adult. The successive differentiation of different cell types that elaborate this complexity results from the activity of gene networks and was likened by Waddington to a flow through a landscape in which valleys represent alternative fates. Geometric methods allow the formal representation of such landscapes and codify the types of behaviors that result from systems of differential equations. Results from Smale and coworkers imply that systems encompassing gene network models can be represented as potential gradients with a Riemann metric, justifying the Waddington metaphor. Here, we extend this representation to include parameter dependence and enumerate all three-way cellular decisions realizable by tuning at most two parameters, which can be generalized to include spatial coordinates in a tissue. All diagrams of cell states vs. model parameters are thereby enumerated. We unify a number of standard models for spatial pattern formation by expressing them in potential form (i.e., as topographic elevation). Turing systems appear nonpotential, yet in suitable variables the dynamics are low dimensional and potential. A time-independent embedding recovers the original variables. Lateral inhibition is described by a saddle point with many unstable directions. A model for the patterning of the Drosophila eye appears as relaxation in a bistable potential. Geometric reasoning provides intuitive dynamic models for development that are well adapted to fit time-lapse data.
Keywords: Morse–Smale; Turing model; Waddington landscape; bifurcation; gene network.
Conflict of interest statement
The authors declare no competing interest.
Figures

References
-
- Smale S., On gradient dynamical systems. Ann. Math. 74, 199–206 (1961).
-
- Meyer K. R., Energy functions for Morse-Smale systems. Am. J. Math. 90, 1031–1040 (1968).
-
- Smale S., Differentiable dynamical systems. Bull. Am. Math. Soc. 73, 747–817 (1967).
-
- Guckenheimer J., Holmes P., Nonlinear Oscillations, Dynamical Systems, and Bifurcations of Vector Fields (Springer Science & Business Media, 2013), vol. 42.
-
- Newhouse S., Peixoto M., There is a simple arc joining any two Morse-Smale flows. Asterisque 31, 15–41 (1976).
Publication types
MeSH terms
Grants and funding
LinkOut - more resources
Full Text Sources
Molecular Biology Databases

