Next generation reservoir computing
- PMID: 34548491
- PMCID: PMC8455577
- DOI: 10.1038/s41467-021-25801-2
Next generation reservoir computing
Abstract
Reservoir computing is a best-in-class machine learning algorithm for processing information generated by dynamical systems using observed time-series data. Importantly, it requires very small training data sets, uses linear optimization, and thus requires minimal computing resources. However, the algorithm uses randomly sampled matrices to define the underlying recurrent neural network and has a multitude of metaparameters that must be optimized. Recent results demonstrate the equivalence of reservoir computing to nonlinear vector autoregression, which requires no random matrices, fewer metaparameters, and provides interpretable results. Here, we demonstrate that nonlinear vector autoregression excels at reservoir computing benchmark tasks and requires even shorter training data sets and training time, heralding the next generation of reservoir computing.
© 2021. The Author(s).
Conflict of interest statement
D.J.G. has financial interests as a cofounder of ResCon Technologies, LCC, which is commercializing RCs. The remaining authors declare no competing interests.
Figures

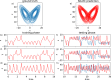
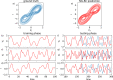
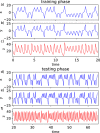
References
-
- Bengio, Y., Boulanger-Lewandowski, N. & Pascanu, R. Advances in optimizing recurrent networks. 2013 IEEE International Conference on Acoustics, Speech and Signal Processing, 2013, pp. 8624–8628 10.1109/ICASSP.2013.6639349 (2013).
Publication types
LinkOut - more resources
Full Text Sources
Other Literature Sources

