Edge current and pairing order transition in chiral bacterial vortices

Abstract

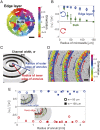
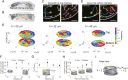
Bacterial suspensions show turbulence-like spatiotemporal dynamics and vortices moving irregularly inside the suspensions. Understanding these ordered vortices is an ongoing challenge in active matter physics, and their application to the control of autonomous material transport will provide significant development in microfluidics. Despite the extensive studies, one of the key aspects of bacterial propulsion has remained elusive: The motion of bacteria is chiral, i.e., it breaks mirror symmetry. Therefore, the mechanism of control of macroscopic active turbulence by microscopic chirality is still poorly understood. Here, we report the selective stabilization of chiral rotational direction of bacterial vortices in achiral circular microwells sealed by an oil/water interface. The intrinsic chirality of bacterial swimming near the top and bottom interfaces generates chiral collective motions of bacteria at the lateral boundary of the microwell that are opposite in directions. These edge currents grow stronger as bacterial density increases, and, within different top and bottom interfaces, their competition leads to a global rotation of the bacterial suspension in a favored direction, breaking the mirror symmetry of the system. We further demonstrate that chiral edge current favors corotational configurations of interacting vortices, enhancing their ordering. The intrinsic chirality of bacteria is a key feature of the pairing order transition from active turbulence, and the geometric rule of pairing order transition may shed light on the strategy for designing chiral active matter.

Keywords: bacterial vortex; chiral active matter; collective motion; microdevices; vortex pairing.

Fig. 1.

Chiral bacterial vortex. (A) Experimental setup: a dense bacterial suspension confined in hydrophilic-treated PDMS microwells and sealed under an oil (32 mPa$\cdot$s)/water (0.8 mPa$\cdot$s) interface stabilized with a surfactant. PEG, polyethylene glycol. (B) Ensemble of chiral bacterial vortices, in microwells with radii $R=35\hspace{0.17em}\mathrm{\mu }\text{m}$ (Top) and $R=20\hspace{0.17em}\mathrm{\mu }\text{m}$ (Bottom) and a height $h=20\hspace{0.17em}\mathrm{\mu }\text{m}$. The bacterial density is 20% vol/vol. Color map codes for the direction of the velocity field. (Scale bar, $100\hspace{0.17em}\mathrm{\mu }\text{m}$.) Schematic illustration of a bacterial vortex in a single microwell. “+” defines the positive sign of CCW rotation. CCW and CW occurrences are displayed with blue and red arrows, respectively.

Fig. 2.

Chiral edge current. (A) Color map of the orientation of collective motion in a chiral bacterial vortex ($R=50\hspace{0.17em}\mathrm{\mu }\text{m}$). The edge layer, defined as the area within $10\hspace{0.17em}\mathrm{\mu }\text{m}$ from the boundary, is separated from the rest of a microwell (the bulk) by a dashed white line. The height of the microwell is $20\hspace{0.17em}\mathrm{\mu }\text{m}$. The bacterial density is 20% vol/vol. (Scale bar, $20\hspace{0.17em}\mathrm{\mu }\text{m}$.) (B) Normalized azimuthal velocity in microwells of various sizes. The blue circles indicate the edge current, and the green squares indicate the motion in bulk. $v_{\theta }$ is averaged over 10 s and plotted with error bars representing SD. (C) Schematic illustration of annulus microchannels within asymmetric conditions. (D) Color map of the orientation of the velocity field in collective motion in annulus microchannels. The height of annulus microchannels is $h=20\hspace{0.17em}\mathrm{\mu }\text{m}$. The bacterial density is 20% vol/vol. (Scale bar, $50\hspace{0.17em}\mathrm{\mu }\text{m}$.) (E) Edge currents in annulus channels with different curvatures. Normalized azimuthal velocities averaged over 10 s are plotted. The blue circles and squares (red circles and squares) indicate the edge current in a CCW direction (in CW direction) that emerges in the channels with the width $w=\hspace{0.17em}50\hspace{0.17em}\mathrm{\mu }\text{m}$ and $w=\hspace{0.17em}100\hspace{0.17em}\mathrm{\mu }\text{m}$, respectively.

Fig. 3.

Chiral edge current as the interplay between the top and bottom interfaces. The radius of microwells is $R=35\hspace{0.17em}\mathrm{\mu }\text{m}$. (Scale bars, $10\hspace{0.17em}\mathrm{\mu }\text{m}$.) (A and B) Schematic illustrations of chiral bacterial swimming (A) near the top oil/water interface and (B) near the bottom water/PDMS interface. Near the top interface, individual bacterial swimming is CCW-biased (blue arrow), while near the bottom interface it is CW-biased (red arrow). (C) Chiral swimming patterns near the wall of a single bacterium beneath the top interface in a dilute condition (0.01% vol/vol, Left) and in a dense condition (20% vol/vol, Right). The bacterial swimming is measured from the top view; their trajectories are indicated by solid lines. The white arrow indicates the heading angle at the end of the track. Scale bars, 10 $\mathrm{\mu }$m. (D) Swimming patterns near the wall of individual bacteria above the bottom interface in dilute (0.01% vol/vol, Left) and dense (20% vol/vol, Right) suspensions. Scale bars, 10 $\mathrm{\mu }$m. (E) Color map of the direction of collective motion at the top and bottom interfaces in microwells of different heights $h$. The bacterial density is 20% vol/vol. (Left) $h=20\hspace{0.17em}\mathrm{\mu }\text{m}$, (Middle) $h=32\hspace{0.17em}\mathrm{\mu }\text{m}$, (Right) $h=49\hspace{0.17em}\mathrm{\mu }\text{m}$. White dashed line indicates the edge layer. (F) Fraction of CCW rotation of individual bacteria within the edge layer in microwells of different heights. Triangle: top interface; inverted triangle: bottom interface. CCW and CW preferences are displayed with blue and red symbols, respectively. (G) The relative number density of bacteria (the ratio of top to bottom) in microwells of different heights. (H) Fraction of CCW rotation of individual bacteria within the edge layer at different bacterial densities. The height is $h=20\hspace{0.17em}\mathrm{\mu }\text{m}$. Sample size and azimuthal velocity of each case in F–H can be found in SI Appendix, Fig. S6. (I) A schematic model for the chiral edge current.

Fig. 4.

Numerical simulation of chiral bacterial vortex. (A) Schematic of the orientation interactions considered in the theoretical model. The upper panel shows the top interface, and the lower panel shows the bottom interface, both from the top view. The chiral self-propelled particles in blue move in the CCW direction, and the red particles move CW. The white arrows indicate the heading angles of the particles. (Left) Along the boundary: polar alignment of the particles near the boundary. The particles move in CCW on the top interface and CW on the bottom interface along the boundary, respectively. (Center) At the same interface: polar alignment of particles moving at the same interface. The radius of the dotted circle indicates the range of the polar alignment, $\epsilon$ ($\epsilon =1$). The particles change their heading angles in the mean direction (dotted arrow). (Right) Between two interfaces: polar alignment of particles between the top and bottom interfaces. The projected area in yellow indicates the effective range of the polar alignment, ${\epsilon }_{tb}\le 1$, projected to the facing interface. The colored arrows represent the rotational velocity of the chiral motion. (B) Numerical simulation of chirality selection in the coupled collective motion of chiral self-propelled particles at various ${\epsilon }_{tb}$. (C) Fraction of CCW rotation of individual particles within the edge layer at various ${\epsilon }_{tb}$. Circle: top interface; asterisk: bottom interface. CCW and CW preferences are displayed with blue and red symbols, respectively.

Fig. 5.

Edge current favors corotational vortex pairing. (A) The corotational vortex pairing (FMV pattern, Top) and the antirotational pairing (AFMV pattern, Bottom). (B) Illustration and definition of relevant geometric parameters. (C) FMV pattern (Left) and AFMV pattern (Right) with edge current. The edge current deviates the orientation angle of bacteria $\theta$ around the tip. (D) Vorticity map of chiral bacterial vortex pairs at various $\mathrm{\Delta }$ with $R=19\hspace{0.17em}\mathrm{\mu }\text{m}$ and $h=20\hspace{0.17em}\mathrm{\mu }\text{m}$. The density of bacteria is 20% vol/vol. (E) The absolute value of the average vorticity of interacting bacterial vortices, with a CCW edge current (inverted black triangles) and without edge current (gray circles), against $\mathrm{\Delta }/R$. Error bar represents SD. Experimental data curves were tested against a sigmoidal function. The transition point of FMV–AFMV patterns is evaluated by the threshold $\left|⟨\mathbf{\Omega }⟩\right|=0.1$.