Entropy Estimation Using a Linguistic Zipf-Mandelbrot-Li Model for Natural Sequences
- PMID: 34573725
- PMCID: PMC8468050
- DOI: 10.3390/e23091100
Entropy Estimation Using a Linguistic Zipf-Mandelbrot-Li Model for Natural Sequences
Abstract
Entropy estimation faces numerous challenges when applied to various real-world problems. Our interest is in divergence and entropy estimation algorithms which are capable of rapid estimation for natural sequence data such as human and synthetic languages. This typically requires a large amount of data; however, we propose a new approach which is based on a new rank-based analytic Zipf-Mandelbrot-Li probabilistic model. Unlike previous approaches, which do not consider the nature of the probability distribution in relation to language; here, we introduce a novel analytic Zipfian model which includes linguistic constraints. This provides more accurate distributions for natural sequences such as natural or synthetic emergent languages. Results are given which indicates the performance of the proposed ZML model. We derive an entropy estimation method which incorporates the linguistic constraint-based Zipf-Mandelbrot-Li into a new non-equiprobable coincidence counting algorithm which is shown to be effective for tasks such as entropy rate estimation with limited data.
Keywords: Zipf–Mandelbrot–Li law; entropy estimation; language models; probabilistic natural sequences.
Conflict of interest statement
The authors declare no conflict of interest.
Figures

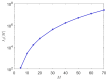
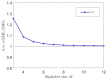
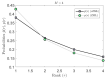




References
-
- Shannon C.E. A Mathematical Theory of Communication (Parts I and II) Bell Syst. Tech. J. 1948;XXVII:379–423. doi: 10.1002/j.1538-7305.1948.tb01338.x. - DOI
-
- Shannon C.E. A Mathematical Theory of Communication (Part III) Bell Syst. Tech. J. 1948;XXVII:623–656. doi: 10.1002/j.1538-7305.1948.tb00917.x. - DOI
-
- Jelinek F., Mercer R.L., Bahl L.R., Baker J.K. Perplexity—A measure of the difficulty of speech recognition tasks. J. Acoust. Soc. Am. 1977;62:S63. doi: 10.1121/1.2016299. - DOI
-
- Shannon C.E. Prediction and Entropy of Printed English. Bell Syst. Tech. J. 1951;30:50–64. doi: 10.1002/j.1538-7305.1951.tb01366.x. - DOI
Grants and funding
LinkOut - more resources
Full Text Sources

