A Drive towards Thermodynamic Efficiency for Dissipative Structures in Chemical Reaction Networks

Abstract

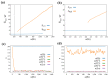
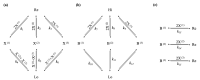
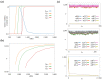
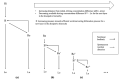
Dissipative accounts of structure formation show that the self-organisation of complex structures is thermodynamically favoured, whenever these structures dissipate free energy that could not be accessed otherwise. These structures therefore open transition channels for the state of the universe to move from a frustrated, metastable state to another metastable state of higher entropy. However, these accounts apply as well to relatively simple, dissipative systems, such as convection cells, hurricanes, candle flames, lightning strikes, or mechanical cracks, as they do to complex biological systems. Conversely, interesting computational properties-that characterize complex biological systems, such as efficient, predictive representations of environmental dynamics-can be linked to the thermodynamic efficiency of underlying physical processes. However, the potential mechanisms that underwrite the selection of dissipative structures with thermodynamically efficient subprocesses is not completely understood. We address these mechanisms by explaining how bifurcation-based, work-harvesting processes-required to sustain complex dissipative structures-might be driven towards thermodynamic efficiency. We first demonstrate a simple mechanism that leads to self-selection of efficient dissipative structures in a stochastic chemical reaction network, when the dissipated driving chemical potential difference is decreased. We then discuss how such a drive can emerge naturally in a hierarchy of self-similar dissipative structures, each feeding on the dissipative structures of a previous level, when moving away from the initial, driving disequilibrium.

Keywords: chemical reaction networks; dissipative structures; stochastic thermodynamics; thermodynamic efficiency.

Figure 1

Nonlinear chemical reaction network, featuring winner-take-all attractor dynamics. Crucially, all three high-concentration nonequilibrium steady states are symmetric with respect to exchanging X⁽¹⁾, X⁽²⁾, and X⁽³⁾. Thus, the associated minimum work-rate required (and the associated minimum driving concentration gradient $$n\left(\mathrm{Hi}\right)-n\left(\mathrm{Lo}\right)$$ to maintain each of these states is the same. (a) Layout of the chemical reaction network (b) Simulations of randomly initialized networks, with driving species clamped at $$n\left(\mathrm{Hi}\right)=500, n\left(\mathrm{Lo}\right)=5$$. Given this forcing, high-concentration states of an individual species $${\mathrm{X}}^{\left(1\right)}$$, $${\mathrm{X}}^{\left(2\right)}$$ or $${\mathrm{X}}^{\left(3\right)}$$, as well as a low-concentration state are stable attractors of the dynamics. (c) Simulations of randomly initialized networks, with driving species clamped at $$n\left(\mathrm{Hi}\right)=100, n\left(\mathrm{Lo}\right)=5$$. Given this forcing, only the low-concentration state constitutes an attractor of the dynamics.

Figure 2

(a,b) Minimum work-rate (equivalent to a minimum concentration difference $$n\left(\mathrm{Hi}\right)-n\left(\mathrm{Lo}\right)$$, where $$n\left(\mathrm{Lo}\right)=5=\mathrm{const}.$$) required to maintain stable nonequilibrium, high-concentration states in a stochastic chemical reaction network featuring winner-take-all dynamics. $$S_{\mathrm{Low}}$$: Low-concentration steady state, $$S_{\mathrm{High}}$$: High-concentration steady state. (c) Representative simulation trajectory for $$n\left(\mathrm{Hi}\right)=200$$. (d) Representative simulation trajectory for $$n\left(\mathrm{Hi}\right)=400$$.

Figure 3

(a) Multi-stable winner-take-all network, featuring a single low- and three high-concentration nonequilibrium steady states, given a sufficiently high-concentration of reservoir species $$\mathrm{Re}$$; (b) Disequilibrium/Free energy reservoir given by the concentration gradient $$n\left(\mathrm{Hi}\right)-n\left(\mathrm{Lo}\right)$$, the dissipation of which is conditional on a high-concentration steady state of the winner-take-all network, by means of the catalysed reaction channels from Hi to B⁽¹⁾, B⁽²⁾, or B⁽³⁾; (c) Bifurcation mechanisms, coupling the dissipative channel to the maintenance of high-concentration states in the winner-take-all network, via the conversion of B⁽¹⁾, B⁽²⁾, or B⁽³⁾ to the reservoir species Re.

Figure 4

Increasing selection pressure on the efficiency of the work-harvesting processes maintaining the dissipative nonequilibrium steady states with decreasing available chemical potential difference. (a) Relative stability of the low and high-concentration steady states as function of $$n\left(\mathrm{Hi}\right)$$, where $$n\left(\mathrm{Lo}\right)=5=\mathrm{const}.$$ (b) Efficiency $$\eta$$ of the bifurcation processes at the individual high-concentration nonequilibrium steady states of species X⁽¹⁾, X⁽²⁾, and X⁽³⁾ as function of $$c\left(\mathrm{Hi}\right)$$, where $$c\left(\mathrm{Lo}\right)=5=\mathrm{const}.$$ (c) Representative trajectories of a chemical reaction network initialized close to each high-concentration steady state for $$n\left(\mathrm{Hi}\right)=1200$$. $$S_{{\mathrm{X}}^{\left(1\right)}}$$: high-concentration state of species X⁽¹⁾, $$S_{{\mathrm{X}}^{\left(2\right)}}$$: high-concentration state of species X⁽²⁾, $$S_{{\mathrm{X}}^{\left(3\right)}}$$: high-concentration state of species X⁽³⁾, $$S_{\mathrm{Low}}$$: Low-concentration steady state.

Figure 5

(a) Schematic depiction of the chemical reaction network discussed in this paper. The nonlinear feedback between the reservoir species Re and the intermediate species $$\mathrm{B}$$ in our simulation is mediated by the dynamics of the winner-take-all module. (b) It is conceivable that a similar dissipative structure develops, which does not feed on the initial driving concentration gradient $$n\left(\mathrm{Hi}\right)-n\left(\mathrm{Lo}\right)$$, but on the structure realizing the dissipative process, in terms of the concentration gradient $$n\left(\mathrm{Re}\right)-n\left(\mathrm{Lo}\right)$$ between the reservoir species of the initial dissipative structure and the low-concentration species. (c) This process could be iterated, by imagining a dissipative structure which now feeds on the reservoir species of the second order dissipative structure. One immediately sees that the concentration gradient available to drive the next layer in such a hierarchy of dissipative structures decreases the further one moves away from the initial driving concentration gradient.