Manipulation of Miniature and Microminiature Bodies on a Harmonically Oscillating Platform by Controlling Dry Friction

Abstract

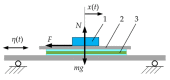
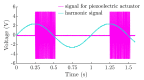
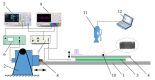
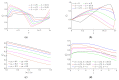
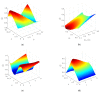
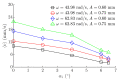
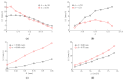
Currently used nonprehensile manipulation systems that are based on vibrational techniques employ temporal (vibrational) asymmetry, spatial asymmetry, or force asymmetry to provide and control a directional motion of a body. This paper presents a novel method of nonprehensile manipulation of miniature and microminiature bodies on a harmonically oscillating platform by creating a frictional asymmetry through dynamic dry friction control. To theoretically verify the feasibility of the method and to determine the control parameters that define the motion characteristics, a mathematical model was developed, and modeling was carried out. Experimental setups for miniature and microminiature bodies were developed for nonprehensile manipulation by dry friction control, and manipulation experiments were carried out to experimentally verify the feasibility of the proposed method and theoretical findings. By revealing how characteristic control parameters influence the direction and velocity, the modeling results theoretically verified the feasibility of the proposed method. The experimental investigation verified that the proposed method is technically feasible and can be applied in practice, as well as confirmed the theoretical findings that the velocity and direction of the body can be controlled by changing the parameters of the function for dynamic dry friction control. The presented research enriches the classical theories of manipulation methods on vibrating plates and platforms, as well as the presented results, are relevant for industries dealing with feeding, assembling, or manipulation of miniature and microminiature bodies.

Keywords: control; dry friction; harmonic oscillations; manipulation; platform; vibrations.

Figure 1

Scheme of nonprehensile manipulation on a harmonically oscillating platform with dry friction control: (1), body to be manipulated; (2), platform; (3), actuators for dry friction control.

Figure 2

Dry friction control in respect of the period of the harmonic excitation.

Figure 3

Experimental setup for manipulation of miniature bodies employing dry friction control: (a) principle diagram: (1), platform; (2), electrodynamic shaker; (3), piezoelectric actuator; (4), manipulation surface; (5), arbitrary waveform generator; (6), power amplifier; (7), piezo linear amplifier; (8), vibration sensor; (9), digital oscilloscope; (10), body to be manipulated; (11), photodiode signal generator; (12), view the oscilloscope screen; (b) general view and a zoomed view of the platform with manipulation surface.

Figure 4

Oscillogram of the synchronized signals of piezoelectric actuator excitation and harmonic excitation when ϕ = 5π/9, λ = π/8, and ω = 62.83 rad/s.

Figure 5

Experimental setup for manipulation of microminiature bodies employing dry friction control: (1), platform; (2), electrodynamic shaker; (3), piezoelectric actuator; (4), manipulation surface; (5), arbitrary waveform generator; (6), power amplifier; (7), piezo linear amplifier; (8), vibration sensor; (9), digital oscilloscope; (10), body to be manipulated (MLCC); (11), high-speed camera; (12), computer.

Figure 6

Non-dimensional average velocity depending on: (a) phase shift ϕ when γ = 4, µ₀ = 0.1, ⟨µ_m⟩/µ₀ = 0.125; (b) λ when γ = 4; µ₀ = 0.1, ⟨µ_m⟩/µ₀ = 0.125; (c) ⟨µ_m⟩/µ₀ when γ = 1, ϕ = π/2, λ = π; (d) γ when µ₀ = 0.1, ⟨µ_m⟩/µ₀ = 0.125.

Figure 7

Three-dimensional representation of non-dimensional average velocity as a function of: (a) ϕ and λ when γ = 1, µ₀ = 0.1, ⟨µ_m⟩/µ₀ = 0.125; (b) µ₀ and ⟨µ_m⟩/µ₀ when ϕ = π/2 λ = π, γ = 1; (c) ϕ and γ when λ = π, µ₀ = 0.1, ⟨µ_m⟩/µ₀ = 0.125; (d) λ and γ when ϕ = π/2, µ₀ = 0.1, ⟨µ_m⟩/µ₀ = 0.125.

Figure 8

Average velocity of the miniature body depending on: (a) phase shift ϕ when A = 0.6 mm, ω = 62.83 rad/s; (b) λ when A = 0.6 mm, ω = 62.83 rad/s; (c) amplitude of the harmonic excitation when ϕ = π/6, λ = 4.1π/9 (d) angular frequency of the harmonic excitation when ϕ = π/6, λ = 4.1π/9.

Figure 9

Average velocity vs. the angle of inclination of the platform when ϕ = π/6, λ = 4.1π/9.

Figure 10

Average velocity of the microminiature body (0805) depending on: (a) phase shift ϕ when A = 0.6 mm, ω = 62.83 rad/s; (b) λ when A = 0.6 mm; ω = 62.83 rad/s; (c) amplitude of the harmonic excitation when ϕ = π/3, λ = 4.1π/9 (d) angular frequency of the harmonic excitation when ϕ = π/3, λ = 4.1π/9.

Figure 11

Captured trajectories of the microminiature body at different values of λ when ϕ = π/10, A = 0.6 mm, ω = 62.83 rad/s.