Skip to main page content
U.S. flag

An official website of the United States government

Dot gov

The .gov means it’s official.
Federal government websites often end in .gov or .mil. Before sharing sensitive information, make sure you’re on a federal government site.

Https

The site is secure.
The https:// ensures that you are connecting to the official website and that any information you provide is encrypted and transmitted securely.

Access keys NCBI Homepage MyNCBI Homepage Main Content Main Navigation
. 2021 Sep 18;13(18):3168.
doi: 10.3390/polym13183168.

A Hierarchical Grid Solver for Simulation of Flows of Complex Fluids

Antonio Castelo  1 , Alexandre M Afonso  2 , Wesley De Souza Bezerra  3
Affiliations

A Hierarchical Grid Solver for Simulation of Flows of Complex Fluids

Antonio Castelo et al. Polymers (Basel). .

Abstract

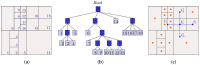
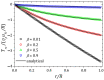
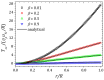
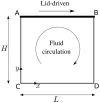
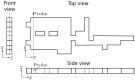
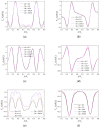
Tree-based grids bring the advantage of using fast Cartesian discretizations, such as finite differences, and the flexibility and accuracy of local mesh refinement. The main challenge is how to adapt the discretization stencil near the interfaces between grid elements of different sizes, which is usually solved by local high-order geometrical interpolations. Most methods usually avoid this by limiting the mesh configuration (usually to graded quadtree/octree grids), reducing the number of cases to be treated locally. In this work, we employ a moving least squares meshless interpolation technique, allowing for more complex mesh configurations, still keeping the overall order of accuracy. This technique was implemented in the HiG-Flow code to simulate Newtonian, generalized Newtonian and viscoelastic fluids flows. Numerical tests and application to viscoelastic fluid flow simulations were performed to illustrate the flexibility and robustness of this new approach.

Keywords: finite difference methods; meshless interpolation; numerical solution; polymer flows; viscoelastic flows.

PubMed Disclaimer

Conflict of interest statement

The authors declare no conflict of interest.

Figures

Figure 1
Figure 1
(a) Example of hierarchical grid. (b) Tree data structure. (c) Finite difference method.
Figure 2
Figure 2
Velocity field for a PTT flow in a pipe.
Figure 3
Figure 3
Shear stress Trx for a PTT flow in a pipe.
Figure 4
Figure 4
Normal stress for a PTT flow in a pipe.
Figure 5
Figure 5
Illustration of lid-driven cavity. The parabolic velocity profile is imposed on the top. The aspect ratio is defined as Λ≡H/L.
Figure 6
Figure 6
Velocity field u obtained along the vertical line x=0.5: (a) De=1.0; (b) De=2.0.
Figure 7
Figure 7
Velocity field v obtained along the horizontal line y=0.75: (a) De=1.0; (b) De=2.0.
Figure 8
Figure 8
Normal stress Txx obtained along the vertical line x=0.5: (a) De=1.0; (b) De=2.0.
Figure 9
Figure 9
Geometry for the complex 3D array of channels.
Figure 10
Figure 10
Streamlines for the complex 3D array of channels. The color scale varies from smallest (blue) to largest (red) velocity magnitude.
Figure 11
Figure 11
Probe views.
Figure 12
Figure 12
Tensor components: (a) Txx; (b) Txy; (c) Tyy; (d) Tyz; (e) Tzz; (f) Txz.
See this image and copyright information in PMC

References

    1. Berger M.J., Oliger J. Adaptive mesh refinement for hyperbolic partial differential equations. J. Comput. Phys. 1984;53:484–512. doi: 10.1016/0021-9991(84)90073-1. - DOI
    1. Popinet S. Gerris: A tree-based adaptive solver for the incompressible Euler equations in complex geometries. J. Comput. Phys. 2003;190:572–600. doi: 10.1016/S0021-9991(03)00298-5. - DOI
    1. Losasso F., Gibou F., Fedkiw R. Simulating Water and Smoke with an Octree Data Structure. ACM Trans. Graph. 2004;23:457–462. doi: 10.1145/1015706.1015745. - DOI
    1. Olshanskii M.A., Terekhov K.M., Vassilevski Y.V. An octree-based solver for the incompressible Navier Stokes equations with enhanced stability and low dissipation. Comput. Fluids. 2013;84:231–246. doi: 10.1016/j.compfluid.2013.04.027. - DOI
    1. Guittet A., Theillard M., Gibou F. A stable projection method for the incompressible Navier-Stokes equations on arbitrary geometries and adaptive Quad/Octrees. J. Comput. Phys. 2015;292:215–238. doi: 10.1016/j.jcp.2015.03.024. - DOI

LinkOut - more resources