Early warning signals of infectious disease transitions: a review
- PMID: 34583561
- PMCID: PMC8479360
- DOI: 10.1098/rsif.2021.0555
Early warning signals of infectious disease transitions: a review
Abstract
Early warning signals (EWSs) are a group of statistical time-series signals which could be used to anticipate a critical transition before it is reached. EWSs are model-independent methods that have grown in popularity to support evidence of disease emergence and disease elimination. Theoretical work has demonstrated their capability of detecting disease transitions in simple epidemic models, where elimination is reached through vaccination, to more complex vector transmission, age-structured and metapopulation models. However, the exact time evolution of EWSs depends on the transition; here we review the literature to provide guidance on what trends to expect and when. Recent advances include methods which detect when an EWS becomes significant; the earlier an upcoming disease transition is detected, the more valuable an EWS will be in practice. We suggest that future work should firstly validate detection methods with synthetic and historical datasets, before addressing their performance with real-time data which is accruing. A major challenge to overcome for the use of EWSs with disease transitions is to maintain the accuracy of EWSs in data-poor settings. We demonstrate how EWSs behave on reported cases for pertussis in the USA, to highlight some limitations when detecting disease transitions with real-world data.
Keywords: critical slowing down; critical transitions; disease elimination; disease emergence; early warning signals; time-series signals.
Figures
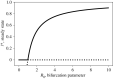
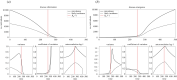
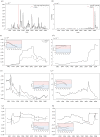
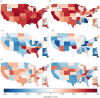
References
-
- World Health Organization. 2002The world health report 2002: reducing risks, promoting healthy life. World Health Organization. See https://apps.who.int/iris/handle/10665/67454. - PubMed
-
- World Health Organization. 2019 Poliomyelitis. See https://www.who.int/news-room/fact-sheets/detail/poliomyelitis (accessed 4 June 2021).
-
- Farrington CP, Andrews NJ, Beale AD, Catchpole MA. 1996A statistical algorithm for the early detection of outbreaks of infectious disease. J. R. Stat. Soc. A (Stat. Soc.) 159, 547-563. (10.2307/2983331) - DOI
-
- Unkel S, Farrington CP, Garthwaite PH, Robertson C, Andrews N. 2012Statistical methods for the prospective detection of infectious disease outbreaks: a review. J. R. Stat. Soc. A (Stat. Soc.) 175, 49-82. (10.1111/rssa.2011.175.issue-1) - DOI
Publication types
MeSH terms
LinkOut - more resources
Full Text Sources
Medical

