Modified Bose-Einstein condensation in an optical quantum gas

Abstract

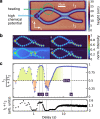
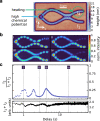
Open quantum systems can be systematically controlled by making changes to their environment. A well-known example is the spontaneous radiative decay of an electronically excited emitter, such as an atom or a molecule, which is significantly influenced by the feedback from the emitter's environment, for example, by the presence of reflecting surfaces. A prerequisite for a deliberate control of an open quantum system is to reveal the physical mechanisms that determine its state. Here, we investigate the Bose-Einstein condensation of a photonic Bose gas in an environment with controlled dissipation and feedback. Our measurements offer a highly systematic picture of Bose-Einstein condensation under non-equilibrium conditions. We show that by adjusting their frequency Bose-Einstein condensates naturally try to avoid particle loss and destructive interference in their environment. In this way our experiments reveal physical mechanisms involved in the formation of a Bose-Einstein condensate, which typically remain hidden when the system is close to thermal equilibrium.

Fig. 1. Photon Bose–Einstein condensation in an open Mach–Zehnder interferometer.

a Microcavity formed by a planar mirror, a nanostructured mirror, and an organic optical medium (top). The optical medium consists of a water-based solution of a dye (rhodamine 6G) and a thermo-responsive polymer (pNIPAM). The height profile of the nanostructured mirror (bottom) creates a potential landscape for the photon gas that effectively acts as a Mach–Zehnder interferometer. A laser beam at a wavelength of 532 nm is used to locally heat the thermo-responsive polymer. This allows for reversible tuning of the local refractive index, which can be used to create optical path length differences in the internal arms of the interferometer. The system is off-resonantly pumped with a tightly focused pulsed laser beam (pulse duration ≃ 5 ns, wavelength 470 nm). The time delay between the heating pulse and the optical pump pulse determines the path length difference that is probed. The photon density within the cavity is determined by measuring the transmitted cavity light with a camera. b Photon density for four time delays. c Normalized switching function I₂/(I₁ + I₂) (upper graph) and total intensity I₁ + I₂ (lower graph) of the open interferometer as a function of the delay between heating and optical pumping (note the logarithmic time axis). Data points are averages over 20 measurements (optical pulses). Error bars indicate the SEM.

Fig. 2. Semi-open Mach–Zehnder interferometer.

a Height map of the nanostructured mirror. b Normalized photon density for four specific time delays between the heating pulse in the upper internal interferometer arm (‘heating’) and the optical pumping (‘high chemical potential’). The observed standing wave mode patterns indicate a superposition of an outgoing and a back reflected wave. c Normalized switching function I₁/(I₁ + 2I₂) (upper graph) and total intensity I₁ + I₂ (lower graph) of the semi-open interferometer. Data points are averages over 20 measurements (optical pulses). Error bars indicate the SEM.

Fig. 3. Closed Mach–Zehnder interferometer.

a Height map of the nanostructured mirror (top). For the results shown, the microcavity is operated in two configurations: plane-parallel and tilted. By tilting one of the microcavity mirrors, a potential gradient is introduced to the photon gas (bottom). This gradient leads to different phase delays for photons that propagate in the different output arms. b Normalized photon density at different time delays for both a plane-parallel and a tilted microresonator. c Normalized switching function I₂/(I₁ + I₂) (upper graph) and total intensity I₁ + I₂ (lower graph) of the closed interferometer in plane-parallel configuration. d Normalized switching function I₂/(I₁ + I₂) (upper graph) and total intensity I₁ + I₂ (lower graph) of the closed interferometer in a tilted configuration. Data points are averages over 20 measurements (optical pulses). Error bars indicate the SEM.

Fig. 4. Closed Mach–Zehnder interferometer with optical path length tuning in the upper output arm.

a Height map of the nanostructured mirror. b Normalized photon density for four specific time delays between the heating pulse in the upper output arm (‘heating’) and the optical pumping (‘high chemical potential’). c Normalized switching function I₂/(I₁ + I₂) (upper graph) and total intensity I₁ + I₂ (lower graph) of the closed interferometer with output arm tuning. Data points are averages over 20 measurements (optical pulses). Errors (SEM) are smaller than the symbol size.