An ensemble reconstruction of global monthly sea surface temperature and sea ice concentration 1000-1849
- PMID: 34608148
- PMCID: PMC8490424
- DOI: 10.1038/s41597-021-01043-1
An ensemble reconstruction of global monthly sea surface temperature and sea ice concentration 1000-1849
Abstract
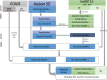
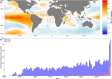
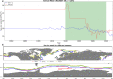
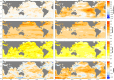
This paper describes a global monthly gridded Sea Surface Temperature (SST) and Sea Ice Concentration (SIC) dataset for the period 1000-1849, which can be used as boundary conditions for atmospheric model simulations. The reconstruction is based on existing coarse-resolution annual temperature ensemble reconstructions, which are then augmented with intra-annual and sub-grid scale variability. The intra-annual component of HadISST.2.0 and oceanic indices estimated from the reconstructed annual mean are used to develop grid-based linear regressions in a monthly stratified approach. Similarly, we reconstruct SIC using analog resampling of HadISST.2.0 SIC (1941-2000), for both hemispheres. Analogs are pooled in four seasons, comprising of 3-months each. The best analogs are selected based on the correlation between each member of the reconstructed SST and its target. For the period 1780 to 1849, We assimilate historical observations of SST and night-time marine air temperature from the ICOADS dataset into our reconstruction using an offline Ensemble Kalman Filter approach. The resulting dataset is physically consistent with information from models, proxies, and observations.
© 2021. The Author(s).
Conflict of interest statement
The authors declare no competing interests.
Figures

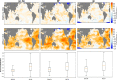


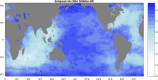
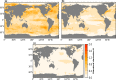
References
-
- Kennedy JJ, Rayner NA, Atkinson CP, Killick RE. An ensemble data set of sea surface temperature change from 1850: The Met Office Hadley Centre HadSST.4.0.0.0 data set. Journal of Geophysical Research: Atmospheres. 2019;124:7719–7763.
-
- Rayner NA, et al. Global analyses of sea surface temperature, sea ice, and night marine air temperature since the late nineteenth century. Journal of Geophysical Research: Atmospheres. 2003;108:D14. doi: 10.1029/2002JD002670. - DOI
-
- Giese BS, Seidel HF, Compo GP, Sardeshmukh PD. An ensemble of ocean reanalyses for 1815–2013 with sparse observational input. J. Geophys. Res. Oceans. 2016;121:6891–6910. doi: 10.1002/2016JC012079. - DOI
-
- Tardif R, et al. Last Millennium Reanalysis with an expanded proxy database and seasonal proxy modeling. Clim. Past. 2019;15:1251–1273. doi: 10.5194/cp-15-1251-2019. - DOI
Grants and funding
- 787574/EC | EU Framework Programme for Research and Innovation H2020 | H2020 Priority Excellent Science | H2020 European Research Council (H2020 Excellent Science - European Research Council)
- 787574/EC | EU Framework Programme for Research and Innovation H2020 | H2020 Priority Excellent Science | H2020 European Research Council (H2020 Excellent Science - European Research Council)
LinkOut - more resources
Full Text Sources

