Technical Note: Break-even dose level for hypofractionated treatment schedules

Abstract

Purpose: To derive the isodose line R relative to the prescription dose below which irradiated normal tissue (NT) regions benefit from a hypofractionated schedule with an isoeffective dose to the tumor. To apply the formalism to clinical case examples.

Methods: From the standard biologically effective dose (BED) equation based on the linear-quadratic (LQ) model, the BED of an NT that receives a relative proportion r of the prescribed dose per fraction for a given α/β-ratio of the tumor, (α/β)_T , and NT, (α/β)_NT , is derived for different treatment schedules while keeping the BED to the tumor constant. Based on this, the "break-even" isodose line R is then derived. The BED of NT regions that receive doses below R decreases for more hypofractionated treatment schedules, and hence a lower risk for NT injury is predicted in these regions. To assess the impact of a linear behavior of BED for high doses per fraction (>6 Gy), we evaluated BED also using the LQ-linear (LQ-L) model.

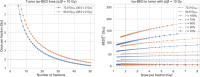
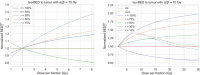
Results: The formalism provides the equations to derive the BED of an NT as function of dose per fraction for an isoeffective dose to the tumor and the corresponding break-even isodose line R. For generic α/β-ratios of (α/β)_T = 10 Gy and (α/β)_NT = 3 Gy and homogeneous dose in the target, R is 30%. R is doubling for stereotactic treatments for which tumor control correlates with the maximum dose of 100% instead of the encompassing isodose line of 50%. When using the LQ-L model, the notion of a break-even dose level R remains valid up to about 20 Gy per fraction for generic α/β-ratios and $D_T=2\left(\alpha /\beta \right)$ .

Conclusions: The formalism may be used to estimate below which relative isodose line R there will be a differential sparing of NT when increasing hypofractionation. More generally, it allows to assess changes of the therapeutic index for sets of isoeffective treatment schedules at different relative dose levels compared to a reference schedule in a compact manner.

Keywords: BED; LQ model; LQ-L model; hypofractionation; isoeffect.

FIGURE 1

Left: Dose per fraction d versus number of fractions n for two sets of treatment schedules (n, d) with iso‐BED to tumor: $S_{72\mathrm{G}{\mathrm{y}}_{10}}$ and $S_{93.6\mathrm{G}{\mathrm{y}}_{10}}$. Right: ${\mathrm{BED}}_3^{\mathrm{IET}}$ for $S_{72\mathrm{G}{\mathrm{y}}_{10}}$ and $S_{93.6\mathrm{G}{\mathrm{y}}_{10}}$ as a function of d for five normal tissue (NT) sparing factors r. In this example, ${\mathrm{BED}}_3^{\mathrm{IET}}$ decreases as dose per fraction increases for NT regions where $r<{(\alpha /\beta )}_{\mathrm{NT}}/{(\alpha /\beta )}_{\mathrm{T}}=30\%$ (see text for more details). Markers indicate integer fraction numbers. Normofractionated treatments with $d=2\mathrm{Gy}$ are indicated by a grey dashed line here and in the following figures.

FIGURE 2

Left: Normalized ${\mathrm{BED}}_3^{\mathrm{IET}}$ for two sets of treatment schedules: ${\mathrm{S}}_{72{\mathrm{Gy}}_{10}}$ and ${\mathrm{S}}_{93.6{\mathrm{Gy}}_{10}}$ as a function of dose per fraction d for five NT sparing factors r and generic α/β‐values. Markers indicate integer fraction numbers. Right: Same as in the left panel, but illustrating the clinical case from Henderson et al. with $S_{170.6{\mathrm{Gy}}_{2.45}}$ (5 × 8 Gy) and α/β‐values of 2.45 Gy (chordoma) and 2.2 Gy (CNS and nerves). In these examples, normalized ${\mathrm{BED}}_3^{\mathrm{IET}}$ and normalized ${\mathrm{BED}}_{2.2}^{\mathrm{IET}}$ decrease as dose per fraction increases for NT regions where $r<{(\alpha /\beta )}_{\mathrm{NT}}/{(\alpha /\beta )}_{\mathrm{T}}$ (see text for more details).

FIGURE 3

Left: Normalized ${\mathrm{BED}}_3^{\mathrm{IET}}$ for two sets of treatment schedules: $S^{50\%}$(t = 50%) and $S^{100\%}$ (t = 100%) as a function of dose per fraction at the encompassing isodose line of 50% for three normal tissue (NT) sparing factors r and generic α/β‐values. Note that r and t are specified relative to the maximum dose per fraction d _max. Right: Normalized ${\mathrm{BED}}_3^{\mathrm{IET}}$ as a function of dose per fraction for doses up to 30 Gy as predicted by the linear‐quadratic (LQ) and the LQ‐linear (LQ‐L) model for five NT sparing factors r and generic α/β‐values.