A Phase Defect Framework for the Analysis of Cardiac Arrhythmia Patterns

Abstract

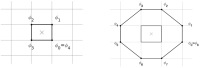
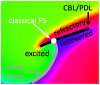
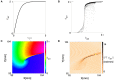
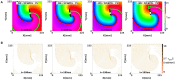
During cardiac arrhythmias, dynamical patterns of electrical activation form and evolve, which are of interest to understand and cure heart rhythm disorders. The analysis of these patterns is commonly performed by calculating the local activation phase and searching for phase singularities (PSs), i.e., points around which all phases are present. Here we propose an alternative framework, which focuses on phase defect lines (PDLs) and surfaces (PDSs) as more general mechanisms, which include PSs as a specific case. The proposed framework enables two conceptual unifications: between the local activation time and phase description, and between conduction block lines and the central regions of linear-core rotors. A simple PDL detection method is proposed and applied to data from simulations and optical mapping experiments. Our analysis of ventricular tachycardia in rabbit hearts (n = 6) shows that nearly all detected PSs were found on PDLs, but the PDLs had a significantly longer lifespan than the detected PSs. Since the proposed framework revisits basic building blocks of cardiac activation patterns, it can become a useful tool for further theory development and experimental analysis.

Keywords: cardiac arrhythmia; non-linear analysis; phase defect; self-organization; spiral wave.

Figure 1

Classical phase analysis of cardiac rotors. (A) Circular-core rotor with Aliev-Panfilov kinetics (Aliev and Panfilov, 1996), where in each point an activation variable u and a recovery variable v are defined. (B) Two observables of the system, V = u and R = v plotted against each other reveal a cycle corresponding to the action potential. The polar angle with respect to a point (V_*, R_*) situated within the cycle serves as a definition of activation phase. (C) Coloring the rotor using phase and a periodic colormap reveals a special point where all phases meet, the phase singularity (PS), see white dot. This point has V = V_*, R = R_*.

Figure 2

Limitations of current PS detection algorithms. (A) Application of the S1-S2 stimulation protocol in the BOCF (Bueno-Orovio et al., 2008) model to initiate a rotor. White dots denoted detected PSs with either a 2 × 2 ring (third panel) or 2 × 2 + 4 × 4 ring (fourth panel) using the method of Kuklik et al. (2017). Both methods identify multiple PS on the CBL (black line). (B) A linear-core rotor in the Fenton Karma model, from 3 perspectives: transmembrane voltage (left), activation phase (middle panel) with PS indicated (white) and LAT (right). (C) Optical mapping of rabbit hearts during ventricular tachycardia showing that detected PSs are all located on CBLs.

Figure 3

Method of PS detection by Kuklik et al. (2017) as used in this paper. Phase differences are considered between pairs of points on a ring of 4 points (Left, 2 × 2 method) or 8 points (Right, 4 × 4 method), to assess whether a PS is present at the central location.

Figure 4

Analysis of a simulated linear-core rotor (BOCF model) using activation phase, showing the WF, WB, classical PSs, and CBL/PDL at different times. The WF and WB were computed as points with V = V_* with positive or negative dV/dt. The CBL/PDL was computed with Equation (4). (A) Transmembrane potential u. The classical PS is located near the position where the WF joins the PDL. At t = 195, several PSs are found near this intersection. (B) Same frames colored with the classical activation phase, showing sudden transitions at WF, WB, and PDL, see gradient of ϕ_act in (C).

Figure 5

Closer look at a linear-core rotor. At the location where classical methods detect a PS, three distinct phases come together: recovered, excited and refractory tissue. At either side of the CBL, two distinct phases are present: refractory vs. either excitable or recovered. Therefore, the CBL is a phase defect line (PDL).

Figure 6

Phase defects shown using the LAT-based phase ϕ_arr. (A) The function ϕ_arr(t_elapsed) from Equation (11). (B) Scatter plot of ϕ_arr vs. ϕ_act, showing that one is a reparameterization of the other on the interval [0, 2π]. (C) Same linear-core rotor in the FK model as in Figure 2B, now shown with ϕ_arr. Note that WF and WB are no longer showing abrupt phase variations, these only happen at the PDL, i.e., the points where conduction block happened. (D) Magnitude of the gradient of ϕ_arr. Due to the discrete sampling of LAT, a staircase artefact in the gradient is seen (no smoothing was applied here).

Figure 7

Analysis of the simulated linear-core rotor from Figure 4 using LAT phase. (A) With ϕ_arr, there are no sudden transitions in phase along the WF and WB, such that only CBLs are shown as phase defects, with large local phase gradient (B).

Figure 8

PSs vs. PDLs in cardiac models and complex analysis. Phases are rendered in-plane (top row) and in 3D, as a Riemannian surface (bottom row). (A) Rigidly rotating spirals, as in the Aliev-Panfilov (AP) reaction-diffusion model (Aliev and Panfilov, 1996) correspond to a PS (gray), similar to the mathematical function ϕ(x, y) = arg(z) shown to the right of it. (B) Linear-core cardiac models, e.g., (Fenton and Karma, 1998) exhibit a PDL or branch cut (black/gray), like the mathematical function $w=f(z)=arg(\sqrt{z^2-1})$ shown to the right of it. Gray areas denote a jump in the phase over a quantity not equal to an integer multiple of 2π, i.e., a PDL (physics) or branch cut (mathematics).

Figure 9

Interpretation of a CBL as a phase defect clarifies why a PS detection finds PSs on it. (A) ϕ_act, rendered in 2D and 3D as a Riemannian surface. (B) ϕ_arr, rendered in 2D and 3D as a Riemannian surface. At the CBL/PDL, the phase surface has a cliff-like appearance.

Figure 10

Creation of a PS from a PDL using a S1-S2 protocol with AP kinetics, showing coexistence of PDL and PS in models that generate circular-core spirals. Snapshots (A–D) shown at times t = 20 ms, t = 38 ms, t = 57 ms, and t = 150 ms.

Figure 11

Analysis of a break-up pattern in a 3D slab geometry with linear-core rotors and rotational anistropy in the FK model. Panels (A–C) show activity at times t = 30, 35, and 40 ms, respectively. The rows show respectively 3D activity with filaments (colors indicate different filaments), normalized transmembrane voltage on the bottom surface, and analysis of the surface patterns in terms of ϕ_arr and ϕ_act and 3D activity with filaments colored as above and PDSs indicated in gray. Note that several phase defects are observed, indicating conduction block near the spiral wave core.

Figure 12

Numerical simulation of rotors in the BOCF model in a biventricular human geometry. (A) Snapshot colored according to normalized transmembrane voltage, showing 2 classical rotor filaments in red. (B) Phase defect surfaces (PDSs) for the same snapshot. The two leftmost PDS bear a classical filament in them, the rightmost one (in the right-ventricular free wall) is a site of conduction block.

Figure 13

Analysis of two-sided optical mapping data in rabbit hearts during ventricular tachycardia. Left: normalized optical intensity (transmembrane voltage) V, together with WF ($V^{*}=0.5,\dot{V}>0$) and wave back ($V^{*}=0.5,\dot{V}<0$). Middle: same data series, ϕ_act computed with R the Hilbert transform of V, with PSs and PDLs computed from ϕ_act. Right: colormap indicates ϕ_arr, computed with τ = 99 ms, equal to the inverse dominant frequency. PSs and PDLs computed from ϕ_arr are also shown. PS detection was done using the 2 × 2 + 4 × 4 method of Kuklik et al. (2017).

Figure 14

Post-processing of rotors observed via optical mapping experiments from n = 6 rabbit hearts. Positive correlation (red line) between number of detected PS and number of points in the PDL for the experiment shown in Figure 13.