Long-Lasting Desynchronization Effects of Coordinated Reset Stimulation Improved by Random Jitters

Abstract

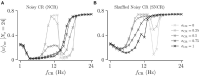
Abnormally strong synchronized activity is related to several neurological disorders, including essential tremor, epilepsy, and Parkinson's disease. Chronic high-frequency deep brain stimulation (HF DBS) is an established treatment for advanced Parkinson's disease. To reduce the delivered integral electrical current, novel theory-based stimulation techniques such as coordinated reset (CR) stimulation directly counteract the abnormal synchronous firing by delivering phase-shifted stimuli through multiple stimulation sites. In computational studies in neuronal networks with spike-timing-dependent plasticity (STDP), it was shown that CR stimulation down-regulates synaptic weights and drives the network into an attractor of a stable desynchronized state. This led to desynchronization effects that outlasted the stimulation. Corresponding long-lasting therapeutic effects were observed in preclinical and clinical studies. Computational studies suggest that long-lasting effects of CR stimulation depend on the adjustment of the stimulation frequency to the dominant synchronous rhythm. This may limit clinical applicability as different pathological rhythms may coexist. To increase the robustness of the long-lasting effects, we study randomized versions of CR stimulation in networks of leaky integrate-and-fire neurons with STDP. Randomization is obtained by adding random jitters to the stimulation times and by shuffling the sequence of stimulation site activations. We study the corresponding long-lasting effects using analytical calculations and computer simulations. We show that random jitters increase the robustness of long-lasting effects with respect to changes of the number of stimulation sites and the stimulation frequency. In contrast, shuffling does not increase parameter robustness of long-lasting effects. Studying the relation between acute, acute after-, and long-lasting effects of stimulation, we find that both acute after- and long-lasting effects are strongly determined by the stimulation-induced synaptic reshaping, whereas acute effects solely depend on the statistics of administered stimuli. We find that the stimulation duration is another important parameter, as effective stimulation only entails long-lasting effects after a sufficient stimulation duration. Our results show that long-lasting therapeutic effects of CR stimulation with random jitters are more robust than those of regular CR stimulation. This might reduce the parameter adjustment time in future clinical trials and make CR with random jitters more suitable for treating brain disorders with abnormal synchronization in multiple frequency bands.

Keywords: coordinated reset stimulation; long-lasting desynchronization; random jitter; spike-timing-dependent plasticity (STDP); stimulation-induced decoupling.

Figure 1

Illustration of stimulation patterns used throughout the manuscript and the resulting distribution of inter-stimulus intervals. (A) Possible realization of NCR stimulation for N_s = 4 stimulation sites. Colored curves indicate the stimulation currents delivered to the individual sites. The pink region marks intervals of possible stimulus onset times, for the maximum jitter σ_CR = 1. The limit of vanishing jitter, σ_CR = 0, corresponds to deterministic stimulus onsets, i.e., CR stimulation. Vertical dashed lines separate subsequent CR cycles, with cycle period T_CR = 1/f_CR. (B) The distribution of inter-stimulus intervals (ISTIs) for NCR stimulation for two values of stimulus jitter, σ_CR. (C) Possible realization of SNCR stimulation with N_s = 4 stimulation sites. The color code is the same as in (A). (D) The distribution of ISTIs for SNCR stimulation for two values of σ_CR.

Figure 2

Theoretical estimates of stimulation-induced weight dynamics and distributions of time lags for different CR stimulation patterns. Individual columns correspond to CR (A), NCR (B), SCR (C), and SNCR (D) stimulation patterns. Panels show the estimated mean rates of weight change $\langle {\mathcal{J}}_X^{\infty }\rangle$, Equation (4), for intrapopulation (A–D) and interpopulation synapses (A'–D'), respectively. Here, X = “intra,” “inter” marks the considered type of synapses. White curves mark zero contour lines and indicate the boundary between strengthening ($\langle {\mathcal{J}}_X^{\infty }\rangle >0$) and weakening of synapses ($\langle {\mathcal{J}}_X^{\infty }\rangle <0$). Corresponding estimates for the distributions of time lags that lead to weight updates $G_X^{\mathrm{\text{A}}}(t)$ (black), Equation (5), are compared to simulation results (red) in (A”–D”) for intrapopulation synapses and in (A”'–D”') for interpopulation synaspes, respectively. In (A”–D”,A”'–D”'), we set N_s = 2 and f_CR = 10 Hz. Networks were simulated for 90 s of ongoing stimulation. Time lags have been recorded from 400 pairs of pre- and postsynaptic neurons. Pairs were sorted according to synapse types “intra” and “inter” and histograms were calculated using a bin size of 1 ms. Theoretical estimates for ${\mathcal{J}}_X^{\infty }$ were obtained by numerical calculations of $p_{\mathrm{\text{X}}}^{\mathrm{\text{A}}}(s)$, Equation (17). To this end, the time interval [−1, 000, 1, 000] ms was discretized using a binsize of dt = 0.01 ms. Then, G_X(t) was obtained using Equation (5). To compare theoretical estimates and simulation results, we plotted G_X(t)dt in (A”–D”,A”'–D”') and normalized the histograms such that counts summed up to two. Parameters: t_d = 3 ms, η = 0.02, τ₊ = 10 ms, τ_R = 4, β = 1.4.

Figure 3

Acute, acute after-, and long-lasting effects of Noisy CR (NCR) with different values of the stimulus jitter, σ_CR, as a function of the stimulation frequency and the number of stimulation sites for strong stimulation. (A–E) Simulation results for the acute mean synaptic weights, 〈w〉_ac, at the end of the 1, 000 s stimulation duration; (A'–E') The acute Kuramoto order parameter, ${\overline{\rho }}_{\mathrm{\text{ac}}}$, time-averaged over the last 10 s of the stimulation duration; (A”–E”) The acute after-effect on synchronization as quantified by the Kuramoto order parameter, ${\overline{\rho }}_{\mathrm{\text{af}}}$, time-averaged over a 10 s interval after cessation of the stimulation; (A”'–E”') Long-lasting desynchronization effects for respective stimulus jitters, as quantified by the Kuramoto order parameter, Equation (2), averaged over a 10 s interval 1,000 s after cessation of stimulation, ${\overline{\rho }}_{\mathrm{\text{ll}}}$. (A,A',A”,A”') show results for σ_CR = 0 which are similar to Kromer et al. (2020) but for longer stimulation durations. The white curves show theoretical estimates of the boundary between weakening and strengthening of interpopulation synapses, see Figure 2. Parameters: The stimulation duration was set to T_stim = 1, 000 s and A_stim = 1.

Figure 4

Acute, acute after-, and long-lasting effects of Shuffled Noisy CR (SNCR) for different values of the stimulus jitter, σ_CR, for strong stimulation as a function of the stimulation frequency and the number of stimulation sites. (A–E) Acute mean synaptic weights, 〈w〉_ac; (A'–E') The acute Kuramoto order parameter, ${\overline{\rho }}_{\mathrm{\text{ac}}}$, time-averaged over the last 10 s of the stimulation; (A”–E”) The acute after-effect of stimulation on synchronization as measured by the Kuramoto order parameter, ${\overline{\rho }}_{\mathrm{\text{af}}}$, time-averaged over an interval of 10 s right after cessation of the stimulation; (A”'–E”') Long-lasting effects of stimulation as quantified by the Kuramoto order parameter, ${\overline{\rho }}_{\mathrm{\text{ll}}}$, time-averaged over a 10 s interval 1, 000 s after cessation of stimulation. Parameters: The stimulation duration was set as T_stim = 1, 000 s and A_stim = 1.

Figure 5

Acute mean synaptic weight for five values of the stimulus jitter, σ_CR, as a function of the stimulation frequency for N_s = 24. (A,B) show results for Noisy CR (NCR) and Shuffled Noisy CR (SNCR), respectively. These graphs represent horizontal lines at N_s = 24 in Figures 3, 4, respectively. Parameters are the same as in Figures 3, 4.

Figure 6

Differences between the outcomes of stimulation with deterministic stimulus onset times (CR/SCR) and NCR/SNCR stimulation with maximum jitter, σ_CR = 1. The difference maps for the acute mean weight (A,B) and for the long-lasting Kuramoto order parameter (A',B'). Parameter regions where NCR/SNCR led to smaller mean weight/values of the long-lasting Kuramoto order parameter compared to CR/SCR are marked red. Dashed vertical lines enclose the largest continuous range of stimulation frequencies where NCR/SNCR stimulation with maximum jitter led to similar or better outcome than CR/SCR stimulation. These frequency ranges are referred to as ${\mathcal{I}}_1$, and ${\mathcal{I}}_2$ in the text. Data are taken from panels A,E (acute mean weight) and A”',E”' (long-lasting Kuramoto order parameters) of Figures 3, 4, respectively.

Figure 7

Acute, acute after-, and long-lasting effects of weak stimulation for the four multisite stimulation protocols. Upper (A–D) show simulation results for the acute mean weight, 〈w〉_ac; (A'–D') show the acute Kuramoto order parameter, ${\overline{\rho }}_{\mathrm{\text{ac}}}$, time-averaged over the last 10 s of the stimulation duration; (A”–D”) show the acute after-effect measured by the Kuramoto order parameter, ${\overline{\rho }}_{\mathrm{\text{af}}}$, 10 s after cessation of the stimulation; and the bottom panels (A”'–D”') show the results for the Kuramoto order parameter, ${\overline{\rho }}_{\mathrm{\text{ll}}}$, time-averaged over a 10 s time interval 1, 000 s after cessation of stimulation. Low values of the Kuramoto order parameter indicate desynchronized activity while high values refer to pronounced in-phase synchronization. The white vertical lines in (A–D) mark a stimulation frequency of f_CR = 12 Hz for which we present a detailed analysis of the influence of the stimulation duration T_stim in Figure 8. The frequency of the original synchronous rhythm is approximately 3.5 Hz and it is shown by the magenta dot-dashed vertical lines. Acute mean weights are measured at the end of T_stim = 500 s stimulation period. Parameters: A_stim = 0.1.

Figure 8

Acute and long-lasting effects of stimulation for different stimulation durations. (A–D) acute mean synaptic weight, 〈w〉_ac, at the end of a stimulation period T_stim for different numbers of stimulation sites N_s. (A'–D') Long-lasting desynchronization effects quantified by the Kuramoto order parameter, ${\overline{\rho }}_{\mathrm{\text{ll}}}$, Equation (2), recorded 1, 000 s after a stimulation period of duration T_stim. Low values indicate desynchronized spiking activity and high values in-phase synchronization of neuronal spiking. Parameters: A_stim = 0.1 and f_CR = 12 Hz.

Figure 9

Long-lasting effects of CR and NCR stimulations as a function of CR frequency, f_CR, and simulation strength, A_stim. (A–D) The long-lasting Kuramoto order parameter for CR stimulation as a function of stimulation frequency and stimulation strength for N_s = 4, 8, 16, and 24. (A'–D') Same as the top row but for NCR with σ_CR = 1. (A”–D”) The difference between the long-lasting Kuramoto order parameter for CR and NCR, $\Delta {\overline{\rho }}_{\mathrm{\text{ll}}}={\overline{rho}}_{\mathrm{\text{ll}}}(\mathrm{\text{CR}})-{\overline{rho}}_{\mathrm{\text{ll}}}(\mathrm{\text{NCR}})$. In the red colored parameter regions, the Kuramoto order parameter for CR was larger than that for NCR, in the blue colored regions CR led to long-lasting desynchronization whereas NCR did not. The columns correspond to different numbers of stimulation sites, N_s = 4, 8, 16, and 24, respectively.

Figure 10

Long-lasting effects of SCR and SNCR stimulation as a function of CR frequency, f_CR, and simulation strength, A_stim. Panels show the long-lasting Kuramoto order parameter for SCR (A–D) and for SNCR (A'–D'). (A”–D”) show the difference between the long-lasting Kuramoto order parameter for SCR and SNCR, $\Delta {\overline{\rho }}_{\mathrm{\text{ll}}}={\overline{rho}}_{\mathrm{\text{ll}}}(\mathrm{\text{SCR}})-{\overline{rho}}_{\mathrm{\text{ll}}}(\mathrm{\text{SNCR}})$. This figure is similar to Figure 9 but for SCR and SNCR.