Mathematical model of STAT signalling pathways in cancer development and optimal control approaches

Abstract

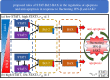
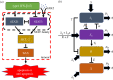
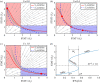
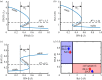
In various diseases, the STAT family display various cellular controls over various challenges faced by the immune system and cell death programs. In this study, we investigate how an intracellular signalling network (STAT1, STAT3, Bcl-2 and BAX) regulates important cellular states, either anti-apoptosis or apoptosis of cancer cells. We adapt a mathematical framework to illustrate how the signalling network can generate a bi-stability condition so that it will induce either apoptosis or anti-apoptosis status of tumour cells. Then, we use this model to develop several anti-tumour strategies including IFN-β infusion. The roles of JAK-STATs signalling in regulation of the cell death program in cancer cells and tumour growth are poorly understood. The mathematical model unveils the structure and functions of the intracellular signalling and cellular outcomes of the anti-tumour drugs in the presence of IFN-β and JAK stimuli. We identify the best injection order of IFN-β and DDP among many possible combinations, which may suggest better infusion strategies of multiple anti-cancer agents at clinics. We finally use an optimal control theory in order to maximize anti-tumour efficacy and minimize administrative costs. In particular, we minimize tumour volume and maximize the apoptotic potential by minimizing the Bcl-2 concentration and maximizing the BAX level while minimizing total injection amount of both IFN-β and JAK2 inhibitors (DDP).

Keywords: STAT1; apoptosis; cancer; mathematical model; optimal control.

Figure 1.

A schematic diagram for a proposed network of apoptosis signalling in the presence of IFN-β/JAK2. (a) Low IFN-β and high JAK2 levels increase STAT3 and Bcl-2 and suppress STAT1 and BAX, maintaining anti-apoptosis status. (b) High IFN-β and decreased JAK2 initiate phenotypical transition from anti-apoptosis to apoptosis of cancer through reversed regulation of each module.

Figure 2.

A schematic diagram of the apoptosis signalling network in figure 1. (a) Key signalling network of apoptosis involving STAT1, STAT3, Bcl-2 and BAX in response to IFN-β and JAK2. (b) The corresponding mathematical model: levels of STAT1 and STAT3, and activity of their target Bcl2, and BAX were represented by ‘S₁’, ‘S₃’, ‘B’ and ‘X’, respectively.

Figure 3.

Dynamics of intracellular (STAT1-STAT3-Bcl2-BAX) module in the absence of JAK2. (a–c) Solution flow of the system (2.9)–(2.12) in the S₁ − S₃ set when S = 0 (a), 0.4 (b) and 1.0 (c). $\mathrm{Filled}\hspace{0.17em}\mathrm{circle}=stable\hspace{0.17em}\mathrm{equilibrium}$, $\mathrm{empty}\hspace{0.17em}\mathrm{circle}=unstable\hspace{0.17em}\mathrm{equilibrium}$. Blue region = upregulation of STAT1 + downregulation of STAT3, pink region = downregulation of STAT1 + upregulation of STAT3. (d) Bifurcation curve of STAT1. Y − axis = equilibrium. W_S = [S^m, S^M] = a window of bi−stabilty.

Figure 4.

Bifurcation diagram and characterization of apoptosis when J = 0. (a–c) Bifurcation curves for steady states of STAT3 (S₃ in (a)), Bcl-2 (B in (b)) and BAX (X in (c)): IFN-β signals (S) provide an on-off switch of STAT3, Bcl-2 and BAX, induing binary modes: malignant and benign progression. W_S = [S^m, S^M] = a window of bi−stabilty. (d) Schematic of anti-apoptosis $({\mathbb{P}}_t)$ and apoptosis $({\mathbb{P}}_a)$ regions in the B − X plane. Parameters: J = 0. Other parameters are given in table 1.

Figure 5.

Intracellular response to IFN-β when J > 0. When J > 0, IFN-β induces uniform responses in intracellular states: downregulation of STAT1/BAX (i.e. $S_1<S_1^{th}$, $X<X^{th},\hspace{0.17em}\mathrm{\forall }S\hspace{0.17em}(0\le S\le 1))$ and upregulation of STAT3/Bcl-2 (i.e. $S_3>S_3^{th}$, $B>B^{th},\hspace{0.17em}\mathrm{\forall }S\hspace{0.17em}(0\le S\le 1))$. Y -axis = steady state (SS) of given variable. Parameters: J = 1. Other parameters are given in table 1.

Figure 6.

Intracellular apoptosis dynamics (STAT1, STAT3, Bcl-2, BAX) in response to IFN-β and therapeutic effect. (a) Time evolution of STAT1 (S₁), STAT3 (S₃), Bcl-2 (B) and BAX (X) after IFN-β treatment (green) at t = 1, 3, 5, 7, 9 with u_S = 15. (b,c) Solution trajectories of the intracellular variables (STAT1-STAT3 in (b) and Bcl-2-BAX in (c)) in the S₁ − S₃ and B − X plane, respectively, with two IFN-β doses: u_S = 0 (red solid), u_S = 15 (blue dotted; corresponding to (a)). Arrow = initial condition, red arrow head = position of solutions with u_S = 0 at final time. blue arrow head = position of solutions with u_S = 15 at final time. (d) Comparison with experimental data: growth patterns of a tumour in control (simulation; solid red curves), and IFN-β-treatment (dashed curves) from our model, control case from experimental (PBS; filled circles), and IFN-β injection case from experimental (filled triangles). (e) Dose response curve when u_S = 0, 2, 4, 6, 8, 10, 15, 20, 40, 60, 100. (f) Average field of STAT1 (blue), STAT3 (red), Bcl-2 (yellow) and BAX (purple) when u_S = 0 (PBS), 10, 15, 100.

Figure 7.

Effect of the injection order of IFN-β and DDP on tumour growth. (a) Normalized tumour volume for 20 different schedules. (b,c) Time courses of the STAT1 (S₁), STAT3 (S₃), Bcl-2 (B) and BAX (X) in response to the ‘SSSDDD’ (b) and ‘DSDDSS’ (c) cases. (d) Dynamics of the tumour size in the ‘SSSDDD’ (solid red) and ‘DSDDSS’ (dashed blue) cases. (e) Average levels of STAT1, STAT3, Bcl-2 and BAX, and tumour volume of all cases in (a) in two categories: schedules with initial injection of IFN-β (left panel), schedules with initial injection of DDP (right panel). (f) Average levels of STAT1, STAT3, Bcl-2 and BAX, and tumour volume of all cases in (a) in two categories: schedules with weighted injection of IFN-β in the first half (left panel), schedules with weighted injection of IFN-β in the second half (right panel).

Figure 8.

(a) The minimum injection dose of IFN-β in the permutation sequences of the two drugs in figure 7, for reduction in the tumour size by 50% compared to the case without IFN-β (control) while h_s is fixed. (b) Maximum resting-time of IFN-β in the permutation sequences of the two drugs, for the same degree of tumour size reduction (50%) compared to the control.

Figure 9.

Effect of duration of IFN-β injection on tumour size. The normalized tumour volume with various duration of IFN-β injection: (a) h_S = 2, (b) h_S = 1, (c) h_S = 0.5 and (d) h_S = 0.1.

Figure 10.

Inhibition of tumour growth by optimal control (Strategy I). (a) Profiles of IFN-β (green, black solid curve) and DDP (pink, black dashed curve) for alternating scheme. (b) Profiles of IFN-β (green, blue solid curve) and DDP (pink, blue dashed curve) for constant scheme. (c) Optimal control profiles of IFN-β (green, solid) and DDP (pink, dashed). (d,e) Time courses of IFN-β (d) and DDP (e) corresponding to three cases in (a–c). (f) Flow of solutions (Bcl-2, BAX) in the phase plane. (g,h) Time evolution of the cumulative injection rates (g) and corresponding tumour size (h) in three cases in (a–c).

Figure 11.

Effect of the half-life of IFN-β on different anti-cancer strategies. Final tumour size in alternative, constant and optimal control strategies with various decay rates of IFN-β (μ_S = 5.5, 4.8*, 3.2). See other parameters in table 1.

Figure 12.

Dynamics of the system corresponding to two alternating schemes of IFN-β and DDP with optimal control. (a,b) Temporal changes in IFN-β infusion in the ‘SSSDDD’ and the ‘DSDDSS’ scheme, respectively. (c) Time courses of the accumulated IFN-β in two cases. (d,e) Time courses of the intracellular molecules (STAT1 (S₁), STAT3 (S₃), Bcl-2 (B) and BAX (X)) in the ‘SSSDDD’ and ‘DSDDSS’ scheme, respectively. The apoptotic state of cancer cells is marked in blue boxes. (f) Reduced tumour sizes of two schemes relative to the base case.