Multi-start Evolutionary Nonlinear OpTimizeR (MENOTR): A hybrid parameter optimization toolbox
- PMID: 34634538
- PMCID: PMC8711798
- DOI: 10.1016/j.bpc.2021.106682
Multi-start Evolutionary Nonlinear OpTimizeR (MENOTR): A hybrid parameter optimization toolbox
Abstract
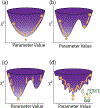
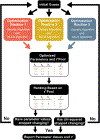
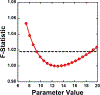
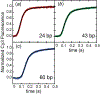
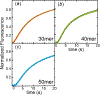
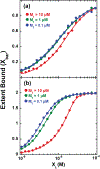
Parameter optimization or "data fitting" is a computational process that identifies a set of parameter values that best describe an experimental data set. Parameter optimization is commonly carried out using a computer program utilizing a non-linear least squares (NLLS) algorithm. These algorithms work by continuously refining a user supplied initial guess resulting in a systematic increase in the goodness of fit. A well-understood problem with this class of algorithms is that in the case of models with correlated parameters the optimized output parameters are initial guess dependent. This dependency can potentially introduce user bias into the resultant analysis. While many optimization programs exist, few address this dilemma. Here we present a data analysis tool, MENOTR, that is capable of overcoming the initial guess dependence in parameter optimization. Several case studies with published experimental data are presented to demonstrate the capabilities of this tool. The results presented here demonstrate how to effectively overcome the initial guess dependence of NLLS leading to greater confidence that the resultant optimized parameters are the best possible set of parameters to describe an experimental data set. While the optimization strategies implemented within MENOTR are not entirely novel, the application of these strategies to optimize parameters in kinetic and thermodynamic biochemical models is uncommon. MENOTR was designed to require minimal modification to accommodate a new model making it immediately accessible to researchers with a limited programming background. We anticipate that this toolbox can be used in a wide variety of data analysis applications. Prototype versions of this toolbox have been used in a number of published investigations already, as well as ongoing work with chemical-quenched flow, stopped-flow, and molecular tweezers data sets. STATEMENT OF SIGNIFICANCE: Non-linear least squares (NLLS) is a common form of parameter optimization in biochemistry kinetic and thermodynamic investigations These algorithms are used to fit experimental data sets and report corresponding parameter values. The algorithms are fast and able to provide good quality solutions for models involving few parameters. However, initial guess dependence is a well-known drawback of this optimization strategy that can introduce user bias. An alternative method of parameter optimization are genetic algorithms (GA). Genetic algorithms do not have an initial guess dependence but are slow at arriving at the best set of fit parameters. Here, we present MENOTR, a parameter optimization toolbox utilizing a hybrid GA/NLLS algorithm. The toolbox maximizes the strength of each strategy while minimizing the inherent drawbacks.
Keywords: Data fitting; Kinetics; Optimization; Thermodynamics.
Copyright © 2021 Elsevier B.V. All rights reserved.
Conflict of interest statement
Declaration of Competing Interest
The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.
Figures

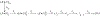
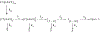
Similar articles
-
Combined genetic algorithm and multiple linear regression (GA-MLR) optimizer: Application to multi-exponential fluorescence decay surface.J Phys Chem A. 2006 Dec 7;110(48):12977-85. doi: 10.1021/jp063998e. J Phys Chem A. 2006. PMID: 17134156
-
An improved hybrid of particle swarm optimization and the gravitational search algorithm to produce a kinetic parameter estimation of aspartate biochemical pathways.Biosystems. 2017 Dec;162:81-89. doi: 10.1016/j.biosystems.2017.09.013. Epub 2017 Sep 23. Biosystems. 2017. PMID: 28951204
-
Speed and convergence properties of gradient algorithms for optimization of IMRT.Med Phys. 2004 May;31(5):1141-52. doi: 10.1118/1.1688214. Med Phys. 2004. PMID: 15191303
-
Fitting enzyme kinetic data with KinTek Global Kinetic Explorer.Methods Enzymol. 2009;467:601-626. doi: 10.1016/S0076-6879(09)67023-3. Methods Enzymol. 2009. PMID: 19897109 Review.
-
Automated neuron model optimization techniques: a review.Biol Cybern. 2008 Nov;99(4-5):241-51. doi: 10.1007/s00422-008-0257-6. Epub 2008 Nov 15. Biol Cybern. 2008. PMID: 19011918 Review.
Cited by
-
NTPs compete in the active site of RNA polymerases I and II.Biophys Chem. 2024 Nov;314:107302. doi: 10.1016/j.bpc.2024.107302. Epub 2024 Aug 3. Biophys Chem. 2024. PMID: 39180852
-
RNA Polymerase I Is Uniquely Vulnerable to the Small-Molecule Inhibitor BMH-21.Cancers (Basel). 2022 Nov 11;14(22):5544. doi: 10.3390/cancers14225544. Cancers (Basel). 2022. PMID: 36428638 Free PMC article.
-
Quantifying the impact of initial RNA primer length on nucleotide addition by RNA polymerase I.Biophys Chem. 2024 Feb;305:107151. doi: 10.1016/j.bpc.2023.107151. Epub 2023 Dec 7. Biophys Chem. 2024. PMID: 38088007 Free PMC article.
-
Integrated Evolutionary Learning: An Artificial Intelligence Approach to Joint Learning of Features and Hyperparameters for Optimized, Explainable Machine Learning.Front Artif Intell. 2022 Apr 5;5:832530. doi: 10.3389/frai.2022.832530. eCollection 2022. Front Artif Intell. 2022. PMID: 35493616 Free PMC article.
-
Reversible Kinetics in Multi-nucleotide Addition Catalyzed by S. cerevisiae RNA polymerase II Reveal Slow Pyrophosphate Release.J Mol Biol. 2024 Jun 15;436(12):168606. doi: 10.1016/j.jmb.2024.168606. Epub 2024 May 8. J Mol Biol. 2024. PMID: 38729258 Free PMC article.
References
-
- Rajendar B, Lucius AL, Molecular mechanism of polypeptide translocation catalyzed by the Escherichia coli ClpA protein translocase, J. Mol. Biol 399 (5) (2010) 665–679. - PubMed
-
- Lucius AL, Jason Wong C, Lohman TM, Fluorescence stopped-flow studies of single turnover kinetics of E. coli RecBCD helicase-catalyzed DNA unwinding, J. Mol. Biol 339 (4) (2004) 731–750. - PubMed
-
- Li T, Lucius AL, Examination of the polypeptide substrate specificity for Escherichia coli ClpA, Biochemistry 52 (29) (2013) 4941–4954. - PubMed
Publication types
MeSH terms
Grants and funding
LinkOut - more resources
Full Text Sources
Research Materials

