A hybrid numeric-analytic solution for pulsed CEST

Abstract

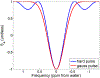
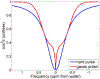
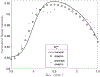
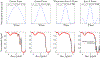
Chemical exchange saturation transfer (CEST) methods measure the effect of magnetization exchange between solutes and water. While CEST methods are often implemented using a train of off-resonant shaped RF pulses, they are typically analyzed as if the irradiation were continuous. This approximation does not account for exchange of rotated magnetization, unique to pulsed irradiation and exploited by chemical exchange rotation transfer methods. In this work, we derive and test an analytic solution for the steady-state water signal under pulsed irradiation by extending a previous work to include the effects of pulse shape. The solution is largely accurate at all offsets, but this accuracy diminishes at higher exchange rates and when applying pulse shapes with large root-mean-squared to mean ratios (such as multi-lobe sinc pulses).

Keywords: CERT; CEST; R1ρ; R2ρ; analytic solution; exchange.

Figure 1:

S as a function of irradiation frequency offset for a hard and gauss-shaped inversion pulse. The hard inversion pulse was 3μT for 3.9ms, with the gauss-shaped pulse amplitude and duration matched to provide the same integrated squared-amplitude and flip angle. A main field strength of 9.4T was assumed.

Figure 2:

⟨cos² β⟩ as a function of irradiation frequency offset for a hard and gauss-shaped inversion pulse. The hard inversion pulse was 3μT for 3.9ms, with the gauss-shaped pulse amplitude and duration matched to provide the same integrated squared-amplitude and flip angle. A main field strength of 9.4T was assumed. Intuitively, the gauss-shaped pulse is more adiabatic in the sense that the magnetization follows the effective field more closely, leading to a higher ⟨cos² β⟩.

Figure 3:

Numeric (i.e., ground-truth) and analytic CEST spectra after a train of 180° pulses. The present solution (∘) closely matches the numeric solution (—) everywhere in the non-exchanging and amide-like exchange cases. For fast-exchanging solutes such as guanidiniums (k_ba ≈ 1000 s⁻¹), the present and previous (•) signal equations both overestimate the CEST effect, but direct water rotation is still captured accurately.

Figure 4:

Numeric (i.e., ground-truth) and analytic CEST spectra after a train of 360° pulses. Results are similar to those in Figure 3, with the exception of slight deviation between the proposed and numeric solutions visible near the water resonance frequency. These deviations are present even in the non-exchanging case, but are small in magnitude in all cases.

Figure 5:

Elimination of ringing near the solute resonance caused by the hard-pulse approximation inherent to Equations 8-11. This figure is a magnification of the spectrum in the central panel of Figure 3; it therefore assumed an amide-like system (δ = 3.5 ppm, k_ba = 50 s⁻¹) and irradiation with average squared-amplitude equivalent to a 1.8 μT continuous wave. Note that the proposed solution captures the numeric solution’s shape more closely than the oscillating spectrum calculated as in reference (1).

Figure 6:

Comparison of the present and the (ground-truth) numeric solutions for different pulse shapes. These figures were generated assuming pulse trains with average irradiation power equivalent to a 1.2μT continuous wave and amide-like exchange characteristics. Because each pulse shape has a different ratio of rms-to-mean amplitude, different duty cycles were employed while pulse repetition time (t_d + t_p) was kept constant at 24.5 ms. All pulse shapes provided well-matched solutions, but pulse shape effects were less damped in the approximation than in the exact solution, especially in more power-intensive pulses such as the five-lobed sinc ("Sinc-5").

Figure 7:

Apparent underdamping of pulse shape effects near the solute resonance following a five-lobed sinc train. This figure contains the same data as (and is a detail of) Figure 6’s bottom right panel. Note that pulse shape effects are largely damped out of the exact solution, but remain in the approximation. This may be caused by the simplifying assumption that rotation exchange does not occur during the pulse.