Skip to main page content
U.S. flag

An official website of the United States government

Dot gov

The .gov means it’s official.
Federal government websites often end in .gov or .mil. Before sharing sensitive information, make sure you’re on a federal government site.

Https

The site is secure.
The https:// ensures that you are connecting to the official website and that any information you provide is encrypted and transmitted securely.

Access keys NCBI Homepage MyNCBI Homepage Main Content Main Navigation
. 2021 Sep 28;21(19):6483.
doi: 10.3390/s21196483.

Sensor Size Effect on Rayleigh Wave Velocity on Cementitious Surfaces

Nicolas Ospitia  1 , Dimitrios G Aggelis  1 , Gerlinde Lefever  1
Affiliations

Sensor Size Effect on Rayleigh Wave Velocity on Cementitious Surfaces

Nicolas Ospitia et al. Sensors (Basel). .

Abstract

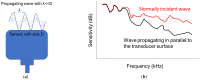
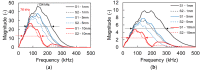
Concrete properties and damage conditions are widely evaluated by ultrasonics. When access is limited, the evaluation takes place from a single surface. In this case, the sensor size plays a crucial role due to the "aperture effect". While this effect is well documented regarding the amplitude or the frequency content of the surface (or Rayleigh) wave pulses, it has not been studied in terms of the wave velocity, although the velocity value is connected to concrete stiffness, porosity, damage degree, and is even empirically used to evaluate compressive strength. In this study, numerical simulations take place where sensors of different sizes are used to measure the surface wave velocity as well as its dependence on frequency (dispersion) and sensor size, showing the strong aperture effect and suggesting rules for reliable measurements on a concrete surface. The numerical trends are also validated by experimental measurements on a cementitious material by sensors of different sizes.

Keywords: aperture effect; concrete; dispersion; heterogeneity; sensor size; surface (Rayleigh) waves.

PubMed Disclaimer

Conflict of interest statement

The authors declare no conflict of interest. The funders had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript; or in the decision to publish the results.

Figures

Figure 1
Figure 1
(a) Illustration of multiple cycles acting simultaneously on the sensor surface and (b) sensitivity vs. frequency curve of a transducer for waves impinging at normal angle and parallel (inspired by [9]).
Figure 2
Figure 2
(a) Schematic representation of a Rayleigh wave on the surface of a medium [17] (the blue arrows stand for the ellipsoidal particle motion) and (b) phase velocity vs. frequency curve for the cases of stiff particles and voids in a cementitious matrix (theoretical results using the scattering model of Waterman and Truel [18]).
Figure 3
Figure 3
Geometry of the simulation model, showing the position of the source and sensors on the specimen.
Figure 4
Figure 4
Displacement field close to the surface of (a) mortar without voids and (b) mortar with 3% voids a few µs after excitation.
Figure 5
Figure 5
Simulated waveforms on homogeneous cement matrix for different apertures and excitation frequency of (a) 50 and (b) 500 kHz.
Figure 6
Figure 6
Simulated waveforms on cement matrix with 3% voids of 2 mm size for different apertures and excitation frequency of (a) 50 and (b) 500 kHz.
Figure 7
Figure 7
Rayleigh dispersion curves for mortar with 0% and 3% voids and excitation frequency of (a) 50, (b) 200, (c) 500 kHz, and (d) theoretical dispersion curve through scattering model.
Figure 8
Figure 8
FFT magnitude of different aperture sensors for excitation frequency of (a) 200 and (b) 500 kHz.
Figure 9
Figure 9
Photographs of surface wave measurements on concrete using different sensors: (a) Mistras pico sensor with 4-mm size, (b) Mistras R15 with 17.35-mm size, and (c) Olympus videoscan with 41.5-mm size.
Figure 10
Figure 10
Typical surface waveforms collected by two sensors for different apertures. The arrows identify characteristic Rayleigh points used for velocity calculations. The vertical axis has been offset for the different apertures for clarity, while the amplitude of the waveforms has not been altered.
Figure 11
Figure 11
(a) Rayleigh dispersion curves on concrete surface with sensors of different apertures and (b) standard deviation of Rayleigh dispersion curves. The arrows indicate the band of lower standard deviation.
See this image and copyright information in PMC

References

    1. Naik T., Malhotra V., Popovics J. Handbook on Nondestructive Testing of Concrete. CRC Press; Boca Raton, FL, USA: 2003. The Ultrasonic Pulse Velocity Method; pp. 8–11.
    1. Landis E., Shah P. Frequency-dependent stress wave attenuation in cement-based materials. J. Eng. Mech. 1995;121:737–743. doi: 10.1061/(ASCE)0733-9399(1995)121:6(737). - DOI
    1. Chaix J.-F., Garnier V., Corneloup G. Ultrasonic wave propagation in heterogeneous solid media: Theoretical analysis and experimental validation. Ultrasonics. 2006;44:200–210. doi: 10.1016/j.ultras.2005.11.002. - DOI - PubMed
    1. Philippidis T., Aggelis D. Experimental study of wave dispersion and attenuation in concrete. Ultrasonics. 2005;43:584–595. doi: 10.1016/j.ultras.2004.12.001. - DOI - PubMed
    1. Iliopoulos S., De Smet L., Aggelis D. Investigating ultrasonic wave dispersion and attenuation in fresh cementitious materials: A combined numerical, analytical, and experimental approach. NDT E Int. 2018;100:115–123. doi: 10.1016/j.ndteint.2018.09.005. - DOI

LinkOut - more resources