Inference for Multiple Heterogeneous Networks with a Common Invariant Subspace
- PMID: 34650343
- PMCID: PMC8513708
Inference for Multiple Heterogeneous Networks with a Common Invariant Subspace
Abstract
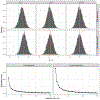
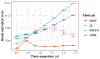
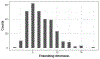
The development of models and methodology for the analysis of data from multiple heterogeneous networks is of importance both in statistical network theory and across a wide spectrum of application domains. Although single-graph analysis is well-studied, multiple graph inference is largely unexplored, in part because of the challenges inherent in appropriately modeling graph differences and yet retaining sufficient model simplicity to render estimation feasible. This paper addresses exactly this gap, by introducing a new model, the common subspace independent-edge multiple random graph model, which describes a heterogeneous collection of networks with a shared latent structure on the vertices but potentially different connectivity patterns for each graph. The model encompasses many popular network representations, including the stochastic blockmodel. The model is both flexible enough to meaningfully account for important graph differences, and tractable enough to allow for accurate inference in multiple networks. In particular, a joint spectral embedding of adjacency matrices-the multiple adjacency spectral embedding-leads to simultaneous consistent estimation of underlying parameters for each graph. Under mild additional assumptions, the estimates satisfy asymptotic normality and yield improvements for graph eigenvalue estimation. In both simulated and real data, the model and the embedding can be deployed for a number of subsequent network inference tasks, including dimensionality reduction, classification, hypothesis testing, and community detection. Specifically, when the embedding is applied to a data set of connectomes constructed through diffusion magnetic resonance imaging, the result is an accurate classification of brain scans by human subject and a meaningful determination of heterogeneity across scans of different individuals.
Keywords: community detection; multiple random graphs; spectral embeddings.
Figures


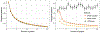



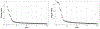

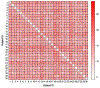

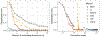
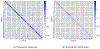
References
-
- Abbe Emmanuel. Community detection and stochastic block models: recent developments. Journal of Machine Learning Research, 18:1–86, 2017.
-
- Arroyo Jesus and Hou Elizabeth. Efficient distributed estimation of inverse covariance matrices. In 2016 IEEE Statistical Signal Processing Workshop (SSP), pages 1–5. IEEE, jun 2016.
-
- Athreya Avanti, Priebe Carey E, Tang Minh, Lyzinski Vince, Marchette David J, and Sussman Daniel L.. A limit theorem for scaled eigenvectors of random dot product graphs. Sankhya A, 78: 1–18, 2016.
Grants and funding
LinkOut - more resources
Full Text Sources
Miscellaneous
