Dynamic Games of Social Distancing During an Epidemic: Analysis of Asymmetric Solutions
- PMID: 34659872
- PMCID: PMC8503885
- DOI: 10.1007/s13235-021-00403-1
Dynamic Games of Social Distancing During an Epidemic: Analysis of Asymmetric Solutions
Abstract
Individual behaviors play an essential role in the dynamics of transmission of infectious diseases, including COVID-19. This paper studies a dynamic game model that describes the social distancing behaviors during an epidemic, assuming a continuum of players and individual infection dynamics. The evolution of the players' infection states follows a variant of the well-known SIR dynamics. We assume that the players are not sure about their infection state, and thus, they choose their actions based on their individually perceived probabilities of being susceptible, infected, or removed. The cost of each player depends both on her infection state and on the contact with others. We prove the existence of a Nash equilibrium and characterize Nash equilibria using nonlinear complementarity problems. We then exploit some monotonicity properties of the optimal policies to obtain a reduced-order characterization for Nash equilibrium and reduce its computation to the solution of a low-dimensional optimization problem. It turns out that, even in the symmetric case, where all the players have the same parameters, players may have very different behaviors. We finally present some numerical studies that illustrate this interesting phenomenon and investigate the effects of several parameters, including the players' vulnerability, the time horizon, and the maximum allowed actions, on the optimal policies and the players' costs.
Keywords: COVID-19 pandemic; Epidemics modeling and control; Games of social distancing; Nash games; Nonlinear complementarity problems.
© The Author(s), under exclusive licence to Springer Science+Business Media, LLC, part of Springer Nature 2021.
Figures




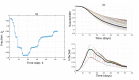
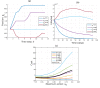
Similar articles
-
An impossibility theorem in game dynamics.Proc Natl Acad Sci U S A. 2023 Oct 10;120(41):e2305349120. doi: 10.1073/pnas.2305349120. Epub 2023 Oct 5. Proc Natl Acad Sci U S A. 2023. PMID: 37796988 Free PMC article.
-
Dynamics to equilibrium in network games: individual behavior and global response.PLoS One. 2015 Mar 24;10(3):e0120343. doi: 10.1371/journal.pone.0120343. eCollection 2015. PLoS One. 2015. PMID: 25803275 Free PMC article.
-
Herd Behaviors in Epidemics: A Dynamics-Coupled Evolutionary Games Approach.Dyn Games Appl. 2022;12(1):183-213. doi: 10.1007/s13235-022-00433-3. Epub 2022 Mar 5. Dyn Games Appl. 2022. PMID: 35281626 Free PMC article.
-
Impact of human cooperation on vaccination behaviors.Heliyon. 2023 May 27;9(6):e16748. doi: 10.1016/j.heliyon.2023.e16748. eCollection 2023 Jun. Heliyon. 2023. PMID: 37292270 Free PMC article.
-
tamasomā jyotirgamaya: Seeking the Self Amidst Covids' Cytokine Cyclones.J Indian Inst Sci. 2020;100(4):663-672. doi: 10.1007/s41745-020-00186-1. Epub 2020 Oct 22. J Indian Inst Sci. 2020. PMID: 33106735 Free PMC article. Review.
Cited by
-
Game-Theoretic Frameworks for Epidemic Spreading and Human Decision-Making: A Review.Dyn Games Appl. 2022;12(1):7-48. doi: 10.1007/s13235-022-00428-0. Epub 2022 Feb 14. Dyn Games Appl. 2022. PMID: 35194521 Free PMC article.
-
Social distancing as a public-good dilemma for socio-economic cost: An evolutionary game approach.Heliyon. 2022 Nov 14;8(11):e11497. doi: 10.1016/j.heliyon.2022.e11497. eCollection 2022 Nov. Heliyon. 2022. PMID: 36411893 Free PMC article.
-
Learning to Mitigate Epidemic Risks: A Dynamic Population Game Approach.Dyn Games Appl. 2023;13(4):1106-1129. doi: 10.1007/s13235-023-00529-4. Epub 2023 Oct 21. Dyn Games Appl. 2023. PMID: 38098859 Free PMC article.
References
-
- Allen LJ, Brauer F, Van den Driessche P, Wu J (2008) Mathematical epidemiology, vol 1945, Springer
-
- Amaral MA, de Oliveira MM, Javarone MA (2020) An epidemiological model with voluntary quarantine strategies governed by evolutionary game dynamics. arXiv preprint arXiv:2008.05979 - PMC - PubMed
-
- Aurell A, Carmona R, Dayanikli G, Lauriere M (2020) Optimal incentives to mitigate epidemics: a Stackelberg mean field game approach. arXiv preprint arXiv:2011.03105
-
- Bertsekas DP (1997) Nonlinear programming. J Oper Res Soc 48(3):334–334
LinkOut - more resources
Full Text Sources
