A Probabilistic Programming Approach to Protein Structure Superposition

Abstract

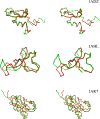
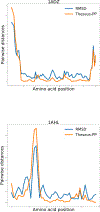
Optimal superposition of protein structures or other biological molecules is crucial for understanding their structure, function, dynamics and evolution. Here, we investigate the use of probabilistic programming to superimpose protein structures guided by a Bayesian model. Our model THESEUS-PP is based on the THESEUS model, a probabilistic model of protein superposition based on rotation, translation and perturbation of an underlying, latent mean structure. The model was implemented in the probabilistic programming language Pyro. Unlike conventional methods that minimize the sum of the squared distances, THESEUS takes into account correlated atom positions and heteroscedasticity (ie. atom positions can feature different variances). THESEUS performs maximum likelihood estimation using iterative expectation-maximization. In contrast, THESEUS-PP allows automated maximum a-posteriori (MAP) estimation using suitable priors over rotation, translation, variances and latent mean structure. The results indicate that probabilistic programming is a powerful new paradigm for the formulation of Bayesian probabilistic models concerning biomolecular structure. Specifically, we envision the use of the THESEUS-PP model as a suitable error model or likelihood in Bayesian protein structure prediction using deep probabilistic programming.

Keywords: Bayesian modelling; deep probabilistic programming; protein structure prediction; protein superposition.

Fig. 1:

The THESEUS-PP model as a Bayesian graphical model. M is the latent, mean structure, which is an N-by-3 coordinate matrix, where N is the number of atoms. t₁ and t₂ are the translations. q is a unit quaternion calculated from three random variables u_0:2 sampled from the unit interval and R is the corresponding rotation matrix. U is the among-row variance matrix of a matrix-normal distribution; X₁ and X₂ are N-by-3 coordinate matrices representing the proteins to be superimposed. Circles denote random variables; squares denote deterministic transformations of random variables. Shaded circles denote observed variables. Capital and small letters represent matrices and vectors respectively.

Fig. 2:

Protein pairs obtained with conventional RMSD superimposition (left) and with THESEUS-PP (right).The protein in green is rotated (X₂). The images are generated with PyMOL [13].

Fig. 2:

Protein pairs obtained with conventional RMSD superimposition (left) and with THESEUS-PP (right).The protein in green is rotated (X₂). The images are generated with PyMOL [13].

Fig. 3:

Graphs showing the pairwise distances (in Å) between the C_α coordinates of the structure pairs. The blue and orange lines represent RMSD and THESEUS-PP superposition, respectively.

Fig. 3:

Graphs showing the pairwise distances (in Å) between the C_α coordinates of the structure pairs. The blue and orange lines represent RMSD and THESEUS-PP superposition, respectively.