The Measurement Error Elephant in the Room: Challenges and Solutions to Measurement Error in Epidemiology

Abstract

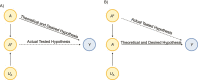
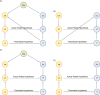
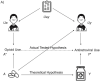
Measurement error, although ubiquitous, is uncommonly acknowledged and rarely assessed or corrected in epidemiologic studies. This review offers a straightforward guide to common problems caused by measurement error in research studies and a review of several accessible bias-correction methods for epidemiologists and data analysts. Although most correction methods require criterion validation including a gold standard, there are also ways to evaluate the impact of measurement error and potentially correct for it without such data. Technical difficulty ranges from simple algebra to more complex algorithms that require expertise, fine tuning, and computational power. However, at all skill levels, software packages and methods are available and can be used to understand the threat to inferences that arises from imperfect measurements.

Keywords: bias correction; epidemiologic methods; epidemiologic review; measurement error; sensitivity analyses.

Figure 1

Classical and Berkson measurement error models. This figure demonstrates 2 measurement error models, highlighting the relationship between the true underlying exposure, A, the measured value A^*, and outcome, Y. A) In the classical measurement error, A^* is influenced by both the exposure construct and some error factor, U_A. Conversely, in (B) the Berkson error model, A varies around A^* with some error function, U_A.

Figure 2

Classical measurement error and extensions to the model. The directed acyclic graphs in the figure illustrate 4 types of measurement error defined based on the ideas of differential versus nondifferential and dependent versus independent error: A) dependent and differential; B) independent and differential; C) dependent and nondifferential; and D) independent and nondifferential. In each example, relationships between true exposure, A, and outcome, Y, are shown, where ^* represents the measured value, affected by the truth and some error term, U, specific to exposure (Ua), outcome (Uy), or both (Uay).

Figure 3

Dependent, differential measurement error. Consider the research question, “Does opioid use increase risk of nonadherence to antiretroviral regimen among people infected with HIV?” In this example, both opioid and antiretroviral use are measured through the same self-reported survey (e.g., a phone call); because the survey is the same measurement tool, this leads to dependent measurement error. In this example, recollection of antiretroviral use (Y) may be systematically different among opioid users and opioid nonusers. Images by various artists from the Noun Project.