Mapping input noise to escape noise in integrate-and-fire neurons: a level-crossing approach

Abstract

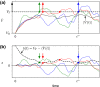
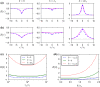
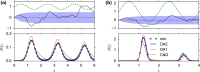
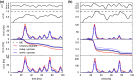
Noise in spiking neurons is commonly modeled by a noisy input current or by generating output spikes stochastically with a voltage-dependent hazard rate ("escape noise"). While input noise lends itself to modeling biophysical noise processes, the phenomenological escape noise is mathematically more tractable. Using the level-crossing theory for differentiable Gaussian processes, we derive an approximate mapping between colored input noise and escape noise in leaky integrate-and-fire neurons. This mapping requires the first-passage-time (FPT) density of an overdamped Brownian particle driven by colored noise with respect to an arbitrarily moving boundary. Starting from the Wiener-Rice series for the FPT density, we apply the second-order decoupling approximation of Stratonovich to the case of moving boundaries and derive a simplified hazard-rate representation that is local in time and numerically efficient. This simplification requires the calculation of the non-stationary auto-correlation function of the level-crossing process: For exponentially correlated input noise (Ornstein-Uhlenbeck process), we obtain an exact formula for the zero-lag auto-correlation as a function of noise parameters, mean membrane potential and its speed, as well as an exponential approximation of the full auto-correlation function. The theory well predicts the FPT and interspike interval densities as well as the population activities obtained from simulations with colored input noise and time-dependent stimulus or boundary. The agreement with simulations is strongly enhanced across the sub- and suprathreshold firing regime compared to a first-order decoupling approximation that neglects correlations between level crossings. The second-order approximation also improves upon a previously proposed theory in the subthreshold regime. Depending on a simplicity-accuracy trade-off, all considered approximations represent useful mappings from colored input noise to escape noise, enabling progress in the theory of neuronal population dynamics.

Keywords: Colored noise; Escape noise; First-passage-time density; Hazard rate; Integrate-and-fire neuron; Interspike interval density; Neuronal population dynamics; Threshold-crossing statistics.

Fig. 1

First-passage time of an integrate-and-fire neuron model and an equivalent model with moving boundary. a At time $t=0$, different realizations of the non-resetting membrane potential $\widehat{V}(t)$ (colored thin lines) are released from the reset potential $V_{\mathrm{R}}$. The non-resetting membrane potential follows a Gaussian process with time-dependent mean $⟨\widehat{V}(t)⟩$ (gray thick line). Shown are three realizations (green, red, blue lines) that have an identical threshold crossing at time $t=t^{\ast }$ (blue circle), which is not necessarily the first crossing (indicated by an arrow). b Transformation to an equivalent time-homogeneous process x(t) with moving boundary b(t), in which the positions of threshold crossings are preserved. Parameters: ${\tau }_{\text{s}}=4$ ms, ${\tau }_{\text{m}}=10$ ms, ${\sigma }_V:={\sigma }_x(\infty )=0.25(V_{\text{T}}-V_{\text{R}})$

Fig. 2

Correlations of level crossings of a stationary process x(t). a Normalized auto-correlation function $R(\tau )\equiv R(t,t+\tau )$ as a function on the time lag $\tau$ (in units of ${\tau }_1\stackrel{\text{def}}{=}{\tau }_{\text{m}}={\gamma }^{-1}$, $\tau \ne 0$) for constant barriers b (as indicated on top) and small time constant ${\tau }_y=0.4{\tau }_{\text{m}}$. The solid magenta lines show the exact semi-analytical result obtained from numerical integration of Eq. (81), and the blue dashed lines show the exponential approximation, Eq. (30), respectively. b Same as a but with ${\tau }_y=2.5{\tau }_{\text{m}}$. c Correlations in the limit of vanishing time lag, $R(0)={lim}_{\tau \to 0}R(\tau )$, as a function of the time scale ratio ${\tau }_2/{\tau }_1={\tau }_y/{\tau }_{\text{m}}$ for three different constant ($\dot{b}=0$) threshold levels b (as indicated). d Correlations for vanishing time lag as a function of the instantaneous threshold level b(t) for three different slopes $\dot{b}(t)$ (at ${\tau }_y=0.4{\tau }_{\text{m}}$): decreasing thresholds lower probability of observing two infinitesimally close level crossings (blue dashed line), whereas increasing threshold increase this probability (finely dashed red line) compared to constant thresholds (solid green line). In all panels, black dotted lines indicate the zero baseline corresponding to a Poisson statistics

Fig. 3

First-passage-time density for periodically moving barrier. a Low amplitude $\alpha =0.25$ (subthreshold regime). Top: illustration of moving barrier (green dashed line) and a sample trajectory x(t) (black solid line). The shaded region indicates the mean $⟨x⟩=0$ (horizontal dashed line) ± the standard deviation ${\sigma }_x(t)$. Bottom: first-passage-time density P(t) from simulations (gray circles) and theory (first- and second-order decoupling approximation—Eq. (13) (green dashed line) and Eq. (7) (blue solid line), respectively; and the Chizhov–Graham theory—Eqs. (96)–(101) (red thin line)). b Same with high amplitude $\alpha =1.2$ (suprathreshold regime). Parameters: ${\sigma }_x(\infty )=0.5$, ${\tau }_x=1$, ${\tau }_y=0.2$, $f=0.5$

Fig. 4

First-passage-time density, survivor function and hazard rate under non-stationary driving of a neuron that fired its last spike at time $\widehat{t}=0$. a Weak subthreshold stimulus $\mu (t)$ (top panel) leads to a mean membrane potential response u(t|0) below threshold at $V_{\text{T}}=1$ (second panel). The first-passage-time density P(t|0) for the first threshold crossing of $\widehat{V}(t)$ is shown in the third panel (gray circles: MC simulations of ${10}^6$ trials; red solid line: Chizhov–Graham theory, Eq. (7), (101); blue dashed line: first-order decoupling approximation (independent up-crossings), Eq. (45), (43); blue solid line: second-order decoupling approximation (correlated upcrossings), Eq. (46), (43). The survival probability $S(t|0)=-dP(t|0)/\text{d}t$ and the corresponding hazard rate $\lambda (t|0)$ are shown in the two bottom panels, respectively. For MC simulations, the hazard rate is computed from the ratio $\lambda (t|0)=P(t|0)/S(t|0)$. b The same for a suprathreshold stimulus, for which the mean membrane potential u(t|0) reaches the threshold. In both figures, ${\tau }_{\text{s}}=4$ ms, ${\tau }_{\text{m}}=10$ ms and ${\sigma }_{\eta }$ is such that the standard deviation of $\widehat{V}$ is ${\sigma }_V=0.25$

Fig. 5

Error of the theoretical approximations for different stimulus properties. The error is measured as the Kolmogorov–Smirnov distance $\mathcal{D}$ between the theoretical and simulated ISI distribution. The stimulus $\mu (t)$ driving the LIF model is sampled from an Ornstein–Uhlenbeck process with mean $\overline{\mu }$, standard deviation $\sqrt{1+{\tau }_{\text{m}}/{\tau }_{\mu }}\overline{\sigma }$ and correlation time ${\tau }_{\mu }$. a Color-coded value of $\mathcal{D}$ as a function of $\overline{\mu }$ and $\overline{\sigma }$ for a rapidly varying stimulus, ${\tau }_{\mu }=1$ ms (left: 1st-order DA , middle: 2nd-order DA, right: Chizhov–Graham theory). b Same as a but for a moderately fast stimulus, ${\tau }_{\mu }=10$ ms. c Same as a but for a slow stimulus, ${\tau }_{\mu }=100$ ms. Other parameters as in Fig. 4

Fig. 6

Macroscopic population activity of non-adapting neurons under non-stationary driving. a Weak subthreshold stimulus $\mu (t)$ (i) as in Fig. 4a leads to a mean membrane potential response $u(t|t_0)$ below threshold at $V_{\text{T}}=1$ (ii). The resulting population activity A(t) is shown in (iii) and (iv) for strong (${\sigma }_V=0.25$) and weak (${\sigma }_V=0.1$) background noise, respectively. Gray circles: MC simulations of ${10}^6$ trials; red solid line: Chizhov–Graham theory, Eq. (7), (101); blue dashed line: level-crossing theory with independent upcrossings (first-order decoupling approximation), Eq. (45), (43); blue solid line: level-crossing theory with correlated upcrossings (second-order decoupling approximation), Eq. (46), (43). b The same for a suprathreshold stimulus as in Fig. 4b, for which the mean membrane potential u(t) reaches the threshold. In both panels, ${\tau }_{\text{s}}=4$ ms, ${\tau }_{\text{m}}=10$ ms, $t_{\text{ref}}=4$ ms and the population was initialized at time $t_0=-25$ ms (initial transient not shown)