The impact of individual variation on abrupt collapses in mutualistic networks

Abstract

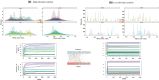
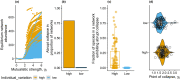
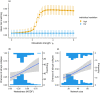
Individual variation is central to species involved in complex interactions with others in an ecological system. Such ecological systems could exhibit tipping points in response to changes in the environment, consequently leading to abrupt transitions to alternative, often less desirable states. However, little is known about how individual trait variation could influence the timing and occurrence of abrupt transitions. Using 101 empirical mutualistic networks, I model the eco-evolutionary dynamics of such networks in response to gradual changes in strength of co-evolutionary interactions. Results indicated that individual variation facilitates the timing of transition in such networks, albeit slightly. In addition, individual variation significantly increases the occurrence of large abrupt transitions. Furthermore, topological network features also positively influence the occurrence of such abrupt transitions. These findings argue for understanding tipping points using an eco-evolutionary perspective to better forecast abrupt transitions in ecological systems.

Keywords: co-evolution; eco-evolutionary dynamics; individual variation; mutualistic networks; population collapses; tipping points.

FIGURE 1

Example co‐evolutionary dynamics of a plant–pollinator mutualistic community for two levels of individual variation. High individual trait variation (a) leads to different eco‐evolutionary dynamics in comparison to when the same plant–pollinator network exhibited low individual trait variation (b). Initial mean trait values were sampled from U[−1,1] and heritability h ² was fixed at 0.4. Trait variance was (a) sampled from random uniform distribution U[0.05, 0.5] and for (b) sampled from U[0.0001, 0.001] and interspecific competition for both plants and pollinators were sampled from random uniform distribution as in Table 1. The total number of species in the example plant–pollinator network was 61

FIGURE 2

Feasibility for three example plant–pollinator networks of different sizes for two levels of individual trait variation. $\log (\mathrm{\rho })$ Quantified the range of interspecific competition coefficients being sampled, with high $\log (\mathrm{\rho })$ values indicating stronger interspecific competition for a given strength of co‐evolutionary interactions ${\gamma }_0$. Network size in (a) was 61, in (b) was 40, and (c) was 11. Heritability in the feasibility analysis was fixed at 0.4 and initial mean trait values were sampled from a random uniform distribution ranging U[−1, 1]. (Note that in the depiction of mutualistic networks the line thickness describing interactions between plants and animals decreases as network size increases in order to accommodate the increasing number of interactions)

FIGURE 3

Individual trait variation on the abruptness of network collapses. (a) Total equilibrium community abundance for 101 plant–pollinator networks for each value of co‐evolutionary mutualistic strength ${\gamma }_0$ and for two levels of individual trait variation. (b) Proportion of networks that collapsed abruptly when species had high individual variation (78%) and when species had low individual variation (0.9%). (c) Fraction of species in a network that exhibited the occurrence of abrupt collapse in the presence of high (mean ± SD error = 17% ± 2.3%) versus low individual variation (mean ± SD error = 0% ± 0%). (d) Violin plots for point of collapse, i.e. the mutualistic strength ${\gamma }_0$ at which the networks collapsed, for two levels of individual phenotypic variation (high and low)

FIGURE 4

(a) Mean trait matching for mutualistic networks for two levels of individual variation. Point estimates of mean trait matching across 101 mutualistic networks as mutualistic strength ${\gamma }_0$ decreased when species had low versus when species had high individual variation. The error bars represent 95% CI. As mutualistic strength decreased gradually, mean trait matching decreased Network topology on chances of occurrence of abrupt collapses: (b) Nestedness (NODF) and (c) network size. Increase in nestedness had a positive influence on occurrence of abrupt collapse. Network size also influenced the occurrence of abrupt collapse of mutualistic networks. Network connectance was highly correlated to both nestedness and network size and hence was dropped from the analysis