Estimation of regional polygenicity from GWAS provides insights into the genetic architecture of complex traits

Abstract

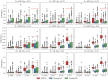
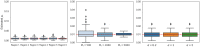
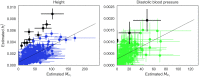
The number of variants that have a non-zero effect on a trait (i.e. polygenicity) is a fundamental parameter in the study of the genetic architecture of a complex trait. Although many previous studies have investigated polygenicity at a genome-wide scale, a detailed understanding of how polygenicity varies across genomic regions is currently lacking. In this work, we propose an accurate and scalable statistical framework to estimate regional polygenicity for a complex trait. We show that our approach yields approximately unbiased estimates of regional polygenicity in simulations across a wide-range of various genetic architectures. We then partition the polygenicity of anthropometric and blood pressure traits across 6-Mb genomic regions (N = 290K, UK Biobank) and observe that all analyzed traits are highly polygenic: over one-third of regions harbor at least one causal variant for each of the traits analyzed. Additionally, we observe wide variation in regional polygenicity: on average across all traits, 48.9% of regions contain at least 5 causal SNPs, 5.44% of regions contain at least 50 causal SNPs. Finally, we find that heritability is proportional to polygenicity at the regional level, which is consistent with the hypothesis that heritability enrichments are largely driven by the variation in the number of causal SNPs.

Fig 1. BEAVR is relatively unbiased in simulated data.

We ran 100 replicates (M = 1, 000 SNPs, N = 500K individuals) where the genome-wide heritability was set to $h_{GW}^2=0.5$ and the true polygenicity of the region was p_r = 0.005, 0.01, 0.05, 0.10. We compared BEAVR to GENESIS-M2 and GENESIS-M3 which employs a spike-and-slab model with either 2 or 3 components (point-mass and either 1 or 2 slabs). All methods are unbiased when the polygenicity is low (p_r = 0.005, 0.01). However, when polygenicity is higher (p_r = 0.05, 0.10), both GENESIS-M2 and GENESIS-M3 are severely downward biased whereas BEAVR provides unbiased estimates across all settings. Dashed red lines denote true regional polygenicity values in each setting.

Fig 2. BEAVR is relatively unbiased across various genetic architectures.

We ran 100 replicates where we vary the genome-wide heritability to be $h_{GW}^2=0.10$, 0.25, 0.5, the polygenicity of the region to be p_r = 0.005, 0.01, 0.05, 0.10, and the sample size N = 50K, 500K, 1 million individuals. We compared BEAVR to GENESIS-M2 (2-component) and GENESIS-M3 (3-component). The x-axis denotes the simulated values for the regional polygenicity and the y-axis denotes the estimated values across 100 replicates. Dashed red lines denote the true regional polygenicity value in each setting.

Fig 3. BEAVR is robust in realistic settings.

(A) Using SNP data from chromosome 22 (M = 9, 564 array SNPs, N = 337K individuals), we simulated 100 replicates where the genome-wide heritability was $h_{GW}^2=0.50$ and p = 0.01. We divided the data into 6-Mb consecutive regions for a total of 6 regions and estimated the regional heritability using external software (HESS [12]). Using BEAVR and the estimated regional heritability, we estimated the regional polygenicity to be unbiased across all regions. (B) We ran 100 replicates where the genome-wide heritability is fixed $h_{GW}^2=0.50$, polygenicity p_r = 0.01, sample size N = 500K, and then varied the number of SNPs in the region from M = 500, 1K, 5K SNPs. We used BEAVR to estimate the polygenicity in each region and found our results to be unbiased across all regions. (C) We set the genome-wide heritability to $h_{GW}^2=0.50$, regional polygenicity p_r = 0.01, and sample size N = 500K. We find that the accuracy of our results is invariant to our choice of prior hyper-parameter (α).

Fig 4. BEAVR is computationally efficient.

(A) We show the run-time in terms of seconds per iteration of the Gibbs sampler (log-scale). We compare the version of BEAVR with the algorithmic speedup outlined in Materials and methods (‘speedup’) versus the straightforward implementation (‘baseline’). We vary the number of SNPs in the region while fixing the polygenicity of each region to p_r = 0.01. (B) We show the runtime of the sampler when the number of SNPs in the region is fixed to M = 1, 000 and we vary the polygenicity.

Fig 5. Distribution of regional polygenicity and heritability.

We divide the genome into 6-Mb regions and report the posterior mean of the regional polygenicity for each region across height and diastolic blood pressure. Using external software [12], we report the distribution of regional heritability for each trait.

Fig 6. Heritability is proportional to the number of causal SNPs in a region.

We show the relationship between the number of causal SNPs and heritability for each region across height and diastolic blood pressure. We fit a linear regression for each trait and report the slope of the regression, which can be interpreted as the increase of heritability per additional causal SNP. Horizontal error bars represent two posterior standard deviations around our estimates for the number of causal SNPs. Vertical error bars represent twice the standard error around the estimates of regional heritability. Dots in black denote outlier regions which have an absolute studentized residual larger than 3.