The Elusive Cochlear Filter: Wave Origin of Cochlear Cross-Frequency Masking

Abstract

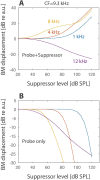
The mammalian cochlea achieves its remarkable sensitivity, frequency selectivity, and dynamic range by spatially segregating the different frequency components of sound via nonlinear processes that remain only partially understood. As a consequence of the wave-based nature of cochlear processing, the different frequency components of complex sounds interact spatially and nonlinearly, mutually suppressing one another as they propagate. Because understanding nonlinear wave interactions and their effects on hearing appears to require mathematically complex or computationally intensive models, theories of hearing that do not deal specifically with cochlear mechanics have often neglected the spatial nature of suppression phenomena. Here we describe a simple framework consisting of a nonlinear traveling-wave model whose spatial response properties can be estimated from basilar-membrane (BM) transfer functions. Without invoking jazzy details of organ-of-Corti mechanics, the model accounts well for the peculiar frequency-dependence of suppression found in two-tone suppression experiments. In particular, our analysis shows that near the peak of the traveling wave, the amplitude of the BM response depends primarily on the nonlinear properties of the traveling wave in more basal (high-frequency) regions. The proposed framework provides perhaps the simplest representation of cochlear signal processing that accounts for the spatially distributed effects of nonlinear wave propagation. Shifting the perspective from local filters to non-local, spatially distributed processes not only elucidates the character of cochlear signal processing, but also has important consequences for interpreting psychophysical experiments.

Keywords: cochlear mechanics; masking; suppression; traveling wave.

Fig. 1

Cartoon illustrating three different classes of cochlear models (panels A–C), and the simple traveling-wave framework (D) employed here to interpret the experimental data.

Fig. 2

(A) BM transfer-function magnitudes (i.e., BM displacement normalized by ear-canal pressure) measured using optical coherence tomography (OCT) in the apex of a mouse cochlea (9.2 kHz region) at various stimulus levels (10 dB steps). The solid lines present transfer functions that have been smoothed using a 3-point zero-phase moving average filter; the dotted lines represent raw recordings. (B) Slopes of the smoothed BM transfer-function magnitudes of panel A, that, in our framework, can be equivalently expressed in dB/Octave (left y-axis) and in dB/mm (right y-axis). Using local scaling, the frequency dependence of the BM transfer function measured at one location can be used to approximate the spatial dependence of the response to a CF tone. The two additional abscissae in panel B show the results of the frequency conversion, expressed as distance from the CF place (mm) and the corresponding CF (kHz). The dotted vertical line marks the CF of the measurement location, and the double-headed arrow indicates the frequency where the 40 dB BM transfer-function slope changes most with level (8.3 kHz). (C) Suppression tuning curve for a 40 dB probe tone, using a 3-dB suppression criterion, averaged over 6 animals. The abscissa is expressed in octaves re CF. The vertical dotted line marks the predicted frequency of maximum suppression, as estimated from the spatial location where the BM transfer-function slope experiences its largest change with level. (D) Suppressor-evoked BM displacement at the suppression threshold level of panel B. Data in C, D from Dewey et al. (2019). The BM transfer functions in panel A have been collected using the methods detailed in Dewey et al. (2019) but with an higher frequency resolution (200 Hz).

Fig. 3

(A) BM transfer-function magnitudes measured in the apex of the mouse cochlea using tones of various levels (10 dB steps, CF=9.8kHz). The solid lines present transfer functions that have been smoothed using a 2-point zero-phase moving average filter; the dotted lines represent unprocessed data. (B) Slopes of the smoothed transfer-function magnitudes shown in panel A. The arrow indicates the frequency (in octaves) of maximal BM gain change with sound level. (C) Suppression (in dB rms) of the click response produced by a moderate-level tone (60 dB SPL) of varying frequency, measured in the same mouse. The vertical dotted line marks the predicted frequency of maximal suppression, as estimated from the slopes of the BM transfer-function magnitudes (see text and Fig. 2).

Fig. 4

(A) BM transfer functions magnitude in a simple 3-D mouse model (see Appendix B) computed for tones of various levels (10 dB steps). For comparison, the open symbols show measured BM transfer functions from Dewey et al. (2019). (B) Slopes of the BM transfer-function magnitudes in dB/octave. The arrow indicates the frequency where the slope changes most with stimulus level above 30 dB (0.1 octaves below CF). (C) Two-tone suppression tuning curve computed for a CF probe tone (30 dB SPL) using a 3-dB suppression criterion. The vertical dashed line in panel C marks the predicted maximal suppression frequency (0.1 octaves above CF), based on the slope analysis in panel C (see text). (D) Suppressor-evoked BM displacement at the recording site for the iso-suppression contours in panel C.

Fig. 5

Suppression produced by notched masking noise on the pressure response of a CF tone. In the spirit of the EQ-NL theorem (de Boer 1997), the effect of the noise was simulated using a quasi-linear approach. In particular, we reduced the parameter [$\tau$ in Eq. (20)] that controls active amplification in the model by 20% at all locations except those with CFs within the notch. Pressure amplification in the model occurs entirely basal to the CF place and the observed suppression therefore depends entirely on the noise above CF. These simulations show that even modest noise-induced activation of the compressive nonlinearity over a spatially distributed region can significantly reduce the pressure driving a given cochlear filter. Although these simulations elucidate the suppressive effects of noise only qualitatively—and conservatively, since the possible effects of tone and noise interaction at the micromechanical level have been neglected—the results illustrate that in notched-noise experiments the signal level at any given cochlear location (filter) depends systematically on the bandwidth of the noise. Thus, contrary to the assumptions of the power-spectrum model of masking, the signal-to-noise ratio at the output of the filter depends on much more than simply the amount of noise that passes through the filter.

Fig. 6

A) Longitudinal and B) cross-sectional geometry of the mouse model. (C) Acoustic area of the scalae of the mouse cochlea, extrapolated from Fig. 5 of Burda et al. (1988). The values are peak-normalized. The solid line represents the data, while the dotted line represents a curve with slope $e^{-x/2l}$, where x is the distance from the cochlear base and l the space constant of the mouse frequency map. (D) Radius of the scalae, extrapolated by fitting a circle to the total cross-sectional area of the scalae (from Fig. 5 of Burda et al. 1988). The dotted line represents a linear fitting function $h=0.13(1-x/L)+0.12$, with L the length of the cochlea (assumed here of 5.2 mm) used to compute the model’s solution. The fitting functions in panels C and D are used to compute the model’s solution [Eqs. (18,19)]

Fig. 7

BM model responses to suppressor and probe tones as a function of suppressor level. The probe is a 40 dB CF-tone (9.3 kHz), while the suppressor level is indicated in the abscissa. The colored lines indicate results obtained using suppressors of different frequencies. A) Overall BM response magnitude, i.e., sum of magnitudes of suppressor and probe frequency components. B) BM magnitude response at the probe frequency. Panel B highlights that a near-CF probe response monotonically decreases with increasing suppressor level—regardless of suppressor frequency. Panel A shows that the overall excitation level of the BM either decreases or increases with suppressor level depending on whether the suppressor frequency is above or below CF, respectively.