Skip to main page content
U.S. flag

An official website of the United States government

Dot gov

The .gov means it’s official.
Federal government websites often end in .gov or .mil. Before sharing sensitive information, make sure you’re on a federal government site.

Https

The site is secure.
The https:// ensures that you are connecting to the official website and that any information you provide is encrypted and transmitted securely.

Access keys NCBI Homepage MyNCBI Homepage Main Content Main Navigation
. 2022;84(2):472-494.
doi: 10.1007/s13571-021-00267-w. Epub 2021 Oct 19.

COVID-19: Optimal Design of Serosurveys for Disease Burden Estimation

Siva Athreya  1 , Giridhara R Babu  2 , Aniruddha Iyer  3 , Mohammed Minhaas B S  3 , Nihesh Rathod  3 , Sharad Shriram  3 , Rajesh Sundaresan  3 , Nidhin Koshy Vaidhiyan  3 , Sarath Yasodharan  3
Affiliations

COVID-19: Optimal Design of Serosurveys for Disease Burden Estimation

Siva Athreya et al. Sankhya B (2008). 2022.

Abstract

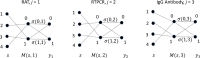
We provide a methodology by which an epidemiologist may arrive at an optimal design for a survey whose goal is to estimate the disease burden in a population. For serosurveys with a given budget of C rupees, a specified set of tests with costs, sensitivities, and specificities, we show the existence of optimal designs in four different contexts, including the well known c-optimal design. Usefulness of the results are illustrated via numerical examples. Our results are applicable to a wide range of epidemiological surveys under the assumptions that the estimate's Fisher-information matrix satisfies a uniform positive definite criterion.

Keywords: COVID-19; Fisher information; adjusted estimate.; c-optimal design; serosurvey; weighted estimate; worst-case design.

PubMed Disclaimer

Conflict of interest statement

Conflict of InterestThe authors have no conflicts of interest to declare that are relevant to the content of this article.

Figures

Figure 1
Figure 1
Noise model for the RAT, RT-PCR, and antibody test outcomes. The left-most subfigure is for RAT, j = 1. The middle subfigure is for the RT-PCR test, j = 2. The right-most figure is for the antibody test, j = 3. In each subfigure, the first connection is a “noiseless” channel indicated by M(s, j). In each subfigure, the second channel is a noisy binary asymmetric channel whose correct outcome probabilities are given by the specificity σ(0, j) and sensitivity σ(1, j). The values are indicated in Table 2. The cross-over probabilities are 1 minus these
See this image and copyright information in PMC

References

    1. Athreya, S., Babu, G.R., Iyer, A., Mohammed Minhaas, B.S., Rathod, N., Shriram, S., Sundaresan, R., Vaidhiyan, N.K. and Yasodharan, S. (2020). Optimal design of serosurveys for disease burden estimation. https://optimaldesign.readiness.in/. - PMC - PubMed
    1. Babu, G. R. et al. (2020). The burden of active infection and anti-SARS-cov-2 IgG antibodies in the general population: Results from a statewide survey in Karnataka, India. medRxiv medRxiv 2020.12.04.20243949. - PMC - PubMed
    1. Bhatia R. Positive definite matrices. India: Hindustan Book Agency; 2007.
    1. Boyd S, Vandenberghe L. Convex optimization. Cambridge: Cambridge University Press; 2004.
    1. Chernoff, H. (1953). Locally optimal designs for estimating parameters. The Annals of Mathematical Statistics, 586–602.

LinkOut - more resources