Robust PCA via Regularized Reaper with a Matrix-Free Proximal Algorithm

Abstract

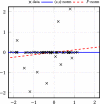
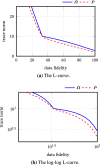
Principal component analysis (PCA) is known to be sensitive to outliers, so that various robust PCA variants were proposed in the literature. A recent model, called reaper, aims to find the principal components by solving a convex optimization problem. Usually the number of principal components must be determined in advance and the minimization is performed over symmetric positive semi-definite matrices having the size of the data, although the number of principal components is substantially smaller. This prohibits its use if the dimension of the data is large which is often the case in image processing. In this paper, we propose a regularized version of reaper which enforces the sparsity of the number of principal components by penalizing the nuclear norm of the corresponding orthogonal projector. If only an upper bound on the number of principal components is available, our approach can be combined with the L-curve method to reconstruct the appropriate subspace. Our second contribution is a matrix-free algorithm to find a minimizer of the regularized reaper which is also suited for high-dimensional data. The algorithm couples a primal-dual minimization approach with a thick-restarted Lanczos process. This appears to be the first efficient convex variational method for robust PCA that can handle high-dimensional data. As a side result, we discuss the topic of the bias in robust PCA. Numerical examples demonstrate the performance of our algorithm.

Keywords: Matrix-free PCA; PCA offset; Regularized reaper; Robust PCA; Thick-restarted Lanczos algorithm.

Fig. 1

Performance of rreaper with (2,1)-norm and Frobenius norm in the data fidelity term, respectively. The first one appears to be more robust against outliers

Fig. 2

Performance of rreaper for different upper dimension estimators $d=10,100$ and regularization parameters $\alpha =\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$4$}\right.,\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.,\raisebox{1ex}{$3$}\!\left/ \!\raisebox{-1ex}{$4$}\right.,1,2$ (top down for each d)

Fig. 3

Mean reconstruction error $||\widehat{\mathit{\Pi }}-{\mathit{\Pi }}_L{||}_{\text{tr}}$ for varying $\alpha$ and d. For every parameter choice, the experiment has been repeated 25 times

Fig. 4

The L-curve for $d=25$ of the data set in Sect. 8.2 consisting of 100 inliers (${\sigma }_{\mathrm{in}}=1$) and 25 outliers (${\sigma }_{\mathrm{out}}=1$) with noise ${\sigma }_{\mathrm{noise}}=0.1$

Fig. 5

The two components of the L-curves in Fig. 4 in dependence of the regularization parameter $\alpha$

Fig. 6

The used data set based on the Extended Yale Face Data Set B and its projections onto the determined subspace using matrix-free rreaper

Fig. 7

Restoration of the first sample by projecting to the principle components determined by several robust PCA’s

Fig. 8

Restoration of the artifact in the first sample by projecting to the principle components determined by several robust PCA’s