NeuroGPU: Accelerating multi-compartment, biophysically detailed neuron simulations on GPUs
- PMID: 34728257
- PMCID: PMC9887806
- DOI: 10.1016/j.jneumeth.2021.109400
NeuroGPU: Accelerating multi-compartment, biophysically detailed neuron simulations on GPUs
Abstract
Background: The membrane potential of individual neurons depends on a large number of interacting biophysical processes operating on spatial-temporal scales spanning several orders of magnitude. The multi-scale nature of these processes dictates that accurate prediction of membrane potentials in specific neurons requires the utilization of detailed simulations. Unfortunately, constraining parameters within biologically detailed neuron models can be difficult, leading to poor model fits. This obstacle can be overcome partially by numerical optimization or detailed exploration of parameter space. However, these processes, which currently rely on central processing unit (CPU) computation, often incur orders of magnitude increases in computing time for marginal improvements in model behavior. As a result, model quality is often compromised to accommodate compute resources.
New method: Here, we present a simulation environment, NeuroGPU, that takes advantage of the inherent parallelized structure of the graphics processing unit (GPU) to accelerate neuronal simulation.
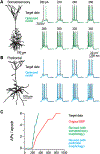
Results & comparison with existing methods: NeuroGPU can simulate most biologically detailed models 10-200 times faster than NEURON simulation running on a single core and 5 times faster than GPU simulators (CoreNEURON). NeuroGPU is designed for model parameter tuning and best performs when the GPU is fully utilized by running multiple (> 100) instances of the same model with different parameters. When using multiple GPUs, NeuroGPU can reach to a speed-up of 800 fold compared to single core simulations, especially when simulating the same model morphology with different parameters. We demonstrate the power of NeuoGPU through large-scale parameter exploration to reveal the response landscape of a neuron. Finally, we accelerate numerical optimization of biophysically detailed neuron models to achieve highly accurate fitting of models to simulation and experimental data.
Conclusions: Thus, NeuroGPU is the fastest available platform that enables rapid simulation of multi-compartment, biophysically detailed neuron models on commonly used computing systems accessible by many scientists.
Keywords: Biophysical simulations; Compartmental models; Conductance-based models; Electrophysiology; Graphical Processing Unit.
Published by Elsevier B.V.
Figures
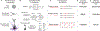
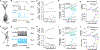
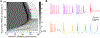

References
-
- Akar NA, Cumming B, Karakasis V, Küsters A, Klijn W, Peyser A, Yates S, 2019. Arbor - A Morphologically-Detailed Neural Network Simulation Library for Contemporary High-Performance Computing Architectures. In: Proceedings - 27th Euromicro International Conference on Parallel, Distributed and Network-Based Processing, PDP 2019, pp 274–282.
-
- Allen NM, Mannion M, Conroy J, Lynch SA, Shahwan A, Lynch B, King MD, 2014. The variable phenotypes of KCNQ-related epilepsy. Epilepsia 55, e99–e105. - PubMed
Publication types
MeSH terms
Grants and funding
LinkOut - more resources
Full Text Sources
Molecular Biology Databases
Research Materials

