Model-Free or Not?

Abstract

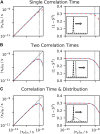
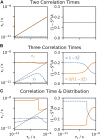
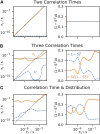
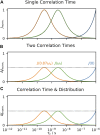
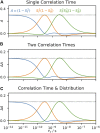
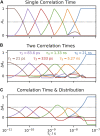
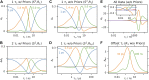
Relaxation in nuclear magnetic resonance is a powerful method for obtaining spatially resolved, timescale-specific dynamics information about molecular systems. However, dynamics in biomolecular systems are generally too complex to be fully characterized based on NMR data alone. This is a familiar problem, addressed by the Lipari-Szabo model-free analysis, a method that captures the full information content of NMR relaxation data in case all internal motion of a molecule in solution is sufficiently fast. We investigate model-free analysis, as well as several other approaches, and find that model-free, spectral density mapping, LeMaster's approach, and our detector analysis form a class of analysis methods, for which behavior of the fitted parameters has a well-defined relationship to the distribution of correlation times of motion, independent of the specific form of that distribution. In a sense, they are all "model-free." Of these methods, only detectors are generally applicable to solid-state NMR relaxation data. We further discuss how detectors may be used for comparison of experimental data to data extracted from molecular dynamics simulation, and how simulation may be used to extract details of the dynamics that are not accessible via NMR, where detector analysis can be used to connect those details to experiments. We expect that combined methodology can eventually provide enough insight into complex dynamics to provide highly accurate models of motion, thus lending deeper insight into the nature of biomolecular dynamics.

Keywords: NMR relaxation; dynamics detectors; model-free analysis; molecular dynamics simulation; solid-state NMR.

FIGURE 1

Complexity of reorientational dynamics. For each bond in a molecule, multiple types of motion result in orientational sampling, where the distribution of angles for each motion result in a generalized order parameter, S ². Therefore, in (A) we plot a possible distribution of Euler angles for a single type of motion (population is plotted as a function of angles β and γ, where α is not required for a symmetric interaction tensor). A single motion is furthermore described by a correlation time, and may be distributed over a range of correlation times. In (B) we plot a possible distribution of correlation times $\left(1-{\mathit{S}}^2\right)\theta \left(\mathit{z}\right)$ , that is, amplitude of motion as a function of the log-correlation time, $\mathit{z}=\mathrm{lo}{\mathrm{g}}_{10}\left({\tau }_c/\mathrm{s}\right)$ . Each distribution is characterized by an amplitude, center, and width. Note that the integral of the distribution is $\left(1-{\mathit{S}}^2\right)$ , S ² being determined by the distribution of angles in (A). While (A,B) illustrate aspects of a single motion, multiple motions influence a given bond, where the total correlation function is the product of individual correlation functions. In (C), we plot four distributions of motion (color). Above each motion, we plot the distribution resulting from the product of that motion and all motions below it (black), eventually resulting in the total distribution seen at the top. Finally, we note that the total distribution varies as a function of position in the molecule, resulting in the 3D plot of the distribution as a function of correlation time and position in the molecule observed in (D). While this is just an illustration, one could imagine that motion in (D) results from three α-helices in a protein, each having a slightly different behavior, and varying dynamics as one approaches the end of each helix.

FIGURE 2

Five distributions of orientations and correlation times that yield the same model-free parameters ( $\left(1-{\mathit{S}}^2\right)$ = 0.3, $\langle {\tau }_e\rangle$ = 0.1 ns). In (A–E), we plot a distribution of orientations (sphere, right); on the axes, we plot the distribution of correlation times resulting from exchange among that set of orientations. Models of motion are wobbling-on-a-cone ( ${\theta }_{\text{cone}}={19}^{°}$ ), wobbling-in-a-cone ( ${\theta }_{\mathrm{cone}}={28}^{°}$ ), symmetric two-site hop ( ${\theta }_{\mathrm{hop}}={39}^{°}$ ), asymmetric two-site hop ( ${\theta }_{\mathrm{hop}}={70}^{°}$ ), and 6-site asymmetric exchange. Insets in (A,B) show correlation times with small amplitudes. $S_{\mathrm{resid}\mathrm{.}}^2$ refers to the order parameter from residual couplings (see Supplementary Section S3), which deviates from the generalized order parameter for asymmetric motion.

FIGURE 3

Model-free fit parameters as a function of input parameters. For each plot, a data set is calculated, using the experiments found in from Table I of Lipari and Szabo (1982b), and the resulting rate constants are fit using the model-free approach, with the resulting ${\langle {\tau }_e\rangle }_{\text{fit}}$ and $\left(1-S^2\right)$ shown on the left and right, respectively. For all plots, the tumbling correlation time is ${\tau }_{\text{M}}$ = 4 ns and $\left(1-S^2\right)$ = 0.3. One correlation time of the internal motion is varied, and we plot ${\langle {\tau }_e\rangle }_{\text{in}}$ on the x-axis. In each plot, we fit using the full spectral density (blue, solid, see Eq. 6) and using a linear approximation (red, dashed, see Eq. 5). In (A), the input correlation function only has a single correlation time. In (B), one correlation time is fixed to 10 ps, and the second correlation time is swept. In (C), a log-Gaussian distribution (μ = 10 ps, σ = 0.75 order of magnitude) is combined with a correlation time that is varied (with total amplitude equal). On the left plots, black dotted lines indicate where the input value, ${\langle {\tau }_e\rangle }_{\text{in}}$ , matches the fit, ${\langle {\tau }_e\rangle }_{\text{fit}}$ . In all plots, vertical black dotted lines indicate where $\omega {\langle {\tau }_e\rangle }_{\text{in}}=0.5$ for $\omega /2\pi$ = 90 MHz, where this frequency corresponds to the highest field used for the data set.

FIGURE 4

EMF parameters as a function of input correlation time (solution-state). For each plot, a data set is calculated, using the set of experiments from Clore et al. (1990), and the resulting rate constants are fitted using the EMF approach. For all plots, ${\tau }_{\text{M}}$ = 8.3 ns, and the input $\left(1-S^2\right)$ = 0.3. In each subplot, the fitted correlation times (left) and amplitudes (right) are shown, as a function of an input correlation time (x-axis). In (A), the input correlation function has two correlation times (with equal amplitudes), with one fixed at 10 ps, and the other swept. In (B), the input correlation function has three correlation times, two fixed at 10 ps and 1 ns, and the third is swept. In (C), a log-Gaussian distribution of correlation times is used (μ = 100 ps, σ = 0.75 orders of magnitude), and a single correlation time is swept. Black dotted lines show the input correlation times (left plots).

FIGURE 5

EMF parameters as a function of input correlation time (solid-state). For each plot, a data set is calculated, including direct measurement of S _resid. via residual couplings (Eq. 17), ¹⁵N T ₁ at 400, 500, and 850 MHz, and T ₂ with MAS of 60 kHz. The resulting rate constants are fitted using the EMF approach. For all plots, $\left(1-S^2\right)$ = 0.3. In each subplot, the fitted correlation times (left) and amplitudes (right) are shown, as a function of an input correlation time (x-axis). In (A), the input correlation function has two correlation times (with equal amplitudes), with one fixed at 3.2 ps, and the other swept. In (B), the input correlation function has three correlation times, two fixed at 3.2 ps and 32 ns, and the third is swept. In (C), a log-Gaussian distribution of correlation times is used (μ = 100 ps, σ = 0.75 orders of magnitude), and a single correlation time is swept. Black dotted lines show the input correlation times (left plots).

FIGURE 6

Behavior of SDM as a function of correlation time. In each subplot, we calculate ¹⁵N T ₁, T ₂, and σ_NH at 600 MHz, and analyze the results using Eq. 21. In (A), the input total correlation function consists of a single decaying exponential term (with amplitude 1), where the terms $J\left(\omega \right)$ are plotted as the correlation time is varied (results are normalized). Black dotted lines show the spectral densities, $J\left(0\right)$ , $J\left({\omega }_{\text{I}}\right)$ , $J\left(0.870{\omega }_{\text{S}}\right)$ , calculated with Eq. 22, and colored lines show the results of the data analysis, yielding an almost exact correspondence. In (B), the total correlation function now uses two correlation times (equal amplitudes), with one fixed at 10 ps, and the second swept (x-axis). On the y-axis, we plot contribution to the terms, $\Delta J\left(\omega \right)$ , from the correlation time being varied. The resulting behavior is identical to that in (A), except that the amplitude is half as large, since we have split the total amplitude between the fixed and variable correlation time (dashed line marks 0.5). In (C), the same information is plotted, but the total correlation function includes a log-Gaussian distribution (μ = 630 ps, σ = 1 order of magnitude), and a single, variable correlation time.

FIGURE 7

Behavior of LeMaster’s approach as a function of correlation time. In each subplot, we calculate ¹⁵N T ₁, T ₂, and σ_NH at 600 MHz for motion with $\left(1-S^2\right)$ = 0.3 and tumbling correlation time of ${\tau }_{\text{M}}$ = 4 ns, and analyze the results using Eq. 24. In (A) the internal correlation function consists of a single decaying exponential term (with amplitude 0.3), where the fitted amplitudes are plotted as the correlation time is varied. In (B) the internal correlation function uses two correlation times (both amplitudes are 0.15), with one correlation time fixed at 10 ps, and the second swept (x-axis). On the y-axis, we plot contributions to the terms from the correlation time being varied. The resulting behavior is identical to that in (A), except that the amplitude is half, since we have split the total amplitude between the fixed and variable correlation time (dashed line marks 0.15). In (C), the same information is plotted, but the total correlation function includes a log-Gaussian distribution (μ = 630 ps, σ = 1 order of magnitude), and a single, variable correlation time.

FIGURE 8

Behavior of the IMPACT approach as a function of correlation time. In each plot, we fit calculated relaxation rate constants, and fit the amplitudes in Eq. 25 according to the IMPACT procedure, using the set of experiments from Khan et al. (2015). In (A), the input total correlation function consists of a single decaying exponential term (with amplitude 1), where the amplitudes are plotted as the correlation time is varied. In (B), the total correlation function uses two correlation times (equal amplitudes), with one fixed at 1 ns, and the second swept (x-axis). On the y-axis, we plot contributions to the $A_k$ from the correlation time being varied. In (C), the same information is plotted, but the total correlation function includes a log-Gaussian distribution (μ = 630 ps, σ = 1 order of magnitude), and a single, variable correlation time.

FIGURE 9

IMPACT behavior in solids. In each plot, we test the behavior of the amplitudes, $A_k$ , using calculated solid-state NMR data (S ², ¹⁵N R ₁, ¹⁵N R _1ρ , with experimental conditions taken from Smith et al. (2016)). (A) plots the behavior of fitting S ² and three R ₁ rate constants to three correlation times (1 ps, 1.4 ns, 5 ns), where the input correlation function has a single correlation time ( $\left(1-S^2\right)$ =0.3), while restricting the $A_k$ to fall between 0 and 1. (B) shows fits under the same conditions, but includes two correlation times, with one fixed at 1 ns, and the other swept (x-axis). The y-axis plots the change in the $A_k$ due to the swept correlation time. (C) shows fits under the same conditions as (A), without restricting the values of the $A_k$ . (D) also removes restrictions on the $A_k$ , but fits S ² and R _1ρ data, using correlation times of (1 ps, 2.5 μs, and 17.8 μs). (E) fits all data (S ², R ₁, R _1ρ ) simultaneously without restrictions on the $A_k$ , with correlation times of 1 ps, 1.4 ns, 5 ns, 2.5 μs, and 17.8 μs (F) fits R ₁ data, but uses one very short correlation time (32 ps), and one very long correlation time (100 ns).

FIGURE 10

Similarity between the CIE XYZ colorspace and the relaxation rate constant space. (A) plots the XYZ colorspace, black lines indicate where single wavelengths fall in the colorspace (z not shown, space is normalized such that x + y + z = 1). Points connected by a triangle indicate the definition of red, green, and blue colors as defined by the sRGB standard (Anderson et al., 1996). (B) plots the sensitivity of the $\overline{x}\left(\lambda \right)$ , $\overline{y}\left(\lambda \right)$ , and $\overline{z}\left(\lambda \right)$ color matching functions as a function of wavelength (λ). (C) plots sRGB sensitivities resulting from transformation from the XYZ to sRGB spaces. Points connected by triangles correspond to definitions of ${\overrightarrow{r}}_1$ , ${\overrightarrow{r}}_2$ , and ${\overrightarrow{r}}_3$ that define the detector space. (D) shows the normalized relaxation rate space for ¹³C R ₁ at 300 and 800 MHz and H–C NOE at 800 MHz. (E) shows the sensitivities of each of these experiments a function of correlation time. (F) shows detector sensitivities resulting from transformation from the relaxation rate constant space to detector space (defined by the points in (D)).

FIGURE 11

Model-free analysis from detectors. (A) shows a detector analysis of HET-s (218–289) fibrils (Smith et al., 2016), with sensitivities shown in (B) (amplitude scale not shown; sensitivities have a maximum of 1). (B) illustrates the procedure to convert 273Ser detector responses into model-free parameters. Bars give the detector responses (y-axis), plotted at the center of the corresponding detector’s sensitivity (x-axis, note that ρ ₀, blue, does not have a well-defined center). At top, we find the ratio of ${\rho }_3^{\left(\theta ,S\right)}/{\rho }_2^{\left(\theta ,S\right)}$ is consistent with a correlation time of 34 ns, with corresponding amplitude of 0.075 (intermediate motion). After subtracting the contribution of this correlation time to ${\rho }_0^{\left(\theta ,S\right)}$ (middle), we find the ratio ${\rho }_1^{\left(\theta ,S\right)}/{\rho }_0^{\left(\theta ,S\right)}$ is consistent with a correlation time of 49 ps, and amplitude of 0.12 (fast motion). Using a fixed correlation time of 14.7 μs, we find an amplitude for the slow motion of 1.8 × 10⁻³ (bottom). (C) shows the results of EMF analysis for all residues using the procedure in (B).

FIGURE 12

Separating population from hop angle and change in chemical shift in NERRD and BMRD experiments. Relevant parameters are shown as insets ( ${\omega }_r/2\pi$ =40 kHz for NERDD plots). In (A–D), contour plots are shown for NERDD and BMRD relaxation rate constants under various conditions, and in each plot, a contour shows all values of $p_1$ and $\theta$ or $\Delta {\omega }_1$ that yield $R_{1\rho }$ equal to the value obtained for $p_1$ = 0.25 and $\theta ={16}^{°}$ or $\Delta {\omega }_{\text{I}}$ = 500 Hz (marked as a cross on each plot). In (E–L), we only show the contour, but for a range of experimental conditions (five experiments, linearly spaced, with range indicated in the plot). In some cases, this yields nearly identical contours, such that we only see one of the five contours.

FIGURE 13

Behavior of fitting R _1ρ data to an offset and a fixed correlation time. (A) shows the offset term, $R_{1\rho }^0$ , divided by 2000, and the order parameter for the slow correlation time, $(1-S_{\text{s}}^2)$ resulting from fitting calculated relaxation rate constants as a function of correlation time to Eq. 36. Experiments are ¹⁵N R _1ρ acquired with MAS frequency of 60 kHz and spin-lock strengths of 11, 16, 25, 38, and 51 kHz, and ${\tau }_{\text{s}}$ is fixed at 18.5 μs. (B) shows detector sensitivities optimized using the same data set. (C) shows $R_{1\rho }^0$ divided by 2000 and $\left(1-S_{\text{s}}^2\right)$ for ¹³C R _1ρ acquired with MAS frequency of 60 kHz and spin-lock strengths of 9, 18, 35, and 48 kHz, as well as an additional experiment with MAS frequency of 40 kHz and spin-lock strength of 25 kHz ${\tau }_{\text{s}}$ is fixed at 7.0 μs. (D) shows detector sensitivities optimized using the same data set.

FIGURE 14

Combining NMR and MD. (A) plots normalized NMR sensitivities for a selection of experiments (S ², ¹⁵N R ₁ at 400, 500, 850 MHz, ¹⁵N R _1ρ at 850 MHz, 60 kHz MAS, ν ₁ at 10, 25, and 45 kHz). (B) shows a linear combination of the normalized sensitivities (x, y positions shifted to reduce plot overlap), which yields the sensitivity of ρ ₂, shown in (C) (green, bold). In color are the weighted contributions from each rate constant, and grey shows the cumulative sum (summing all sensitivities at and below the grey line). (C) shows the five sensitivities optimized from NMR data. (D) plots sensitivities of time points from MD-derived correlation functions (0 s, 10 points log-spaced from 50 ps to 1 μs). (E) shows a linear combination of those sensitivities, optimized to match the sensitivity of ρ ₂ (x, y positions shifted to reduce plot overlap). (F) shows detectors optimized to match the NMR-derived detectors in (C). (G) shows spatial correlation of motion in a helix as a function of correlation time (windows for <20, ∼20, ∼100, ∼800 ns). Color intensity and bond radii indicate the correlation coefficient between that residue’s H–N motion and the motion of the black residue. (H) illustrates frames used to separate transformation from the PAS to the lab frame into four steps: a peptide plane frame, a helix frame, and a molecule frame (illustration inspired by Brown (1996), molecule plots created with ChimeraX (Pettersen et al., 2021)).