SU(2) hadrons on a quantum computer via a variational approach

Abstract

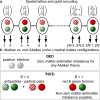
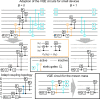
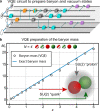
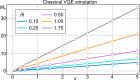
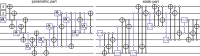
Quantum computers have the potential to create important new opportunities for ongoing essential research on gauge theories. They can provide simulations that are unattainable on classical computers such as sign-problem afflicted models or time evolutions. In this work, we variationally prepare the low-lying eigenstates of a non-Abelian gauge theory with dynamically coupled matter on a quantum computer. This enables the observation of hadrons and the calculation of their associated masses. The SU(2) gauge group considered here represents an important first step towards ultimately studying quantum chromodynamics, the theory that describes the properties of protons, neutrons and other hadrons. Our calculations on an IBM superconducting platform utilize a variational quantum eigensolver to study both meson and baryon states, hadrons which have never been seen in a non-Abelian simulation on a quantum computer. We develop a hybrid resource-efficient approach by combining classical and quantum computing, that not only allows the study of an SU(2) gauge theory with dynamical matter fields on present-day quantum hardware, but further lays out the premises for future quantum simulations that will address currently unanswered questions in particle and nuclear physics.

Fig. 1. Gauge theory on a lattice.

To study the SU(2) theory in one dimension, we employ the spatial lattice in (a), where each site consists of either matter or antimatter particles of the two possible colors. In the equivalent qubit formulation, each particle is represented by a qubit on a one-dimensional chain, which hence contains a number of qubits that equals twice the number of staggered sites. For a full discussion of the qubit representation see Supplementary Fig. 1. b Illustrates a comparison between the different gauge invariant states allowed in the neutral charge sector of Abelian QED and SU(2). While in the Abelian case neutral states require an equal number of matter (full spheres) and antimatter (striped spheres) particles, in the non-Abelian case, color-neutral states with a non-zero matter-antimatter imbalance are possible.

Fig. 2. VQE ansatz circuits.

The uppermost circuits for N = 4 can be reduced by absorbing the static colored gates into ${\widehat{U}}_s$. The parametrized controlled gates are Y-rotations. For the orange gates, the circuit identity in the orange box has to be applied beforehand. This results in inactive qubits (dashed lines), which do not need to be physically available on the quantum device. Details of circuit reduction are discussed in Methods. In the lower left, the introduced SWAP gate for the adaptation to the architecture of the ibmq_casablanca processor is shown, with the qubit labeling as introduced in Fig. 3a (see below). The N = 2 circuits to estimate the meson mass are illustrated in the box in the bottom right.

Fig. 3. VQE calculation of a baryon.

We variationally study an effective eight sites chain with the experimental circuit shown in (a). The boxes represent single-qubit gates. Gray boxes are fixed gates while the color coding indicates dependence from three variational parameters. Their exact implementation changes depending on the combination of the parameter values, which is automatically compiled from the original circuit shown in Fig. 2. This takes into account the coupling topology of the IBMQ Casablanca processor, which, together with the qubit identification for the B = 0 sector are shown on the left. b The circuit yields the mass of the baryon (error bars are smaller than markers, see “Methods” for a more detailed discussion), an SU(2)-"proton” (see inset), for a range of x and $\tilde{m}=1$ as explained in the main text.

Fig. 4. VQE calculation of the meson mass.

To obtain the low-lying energy spectrum as shown in (a), we first employ the circuit in (b) to obtain the vacuum energy E_v (circles) in step I. Note that the employed gates are either rotations around the y-axis, the corresponding controlled gate, and bitflip X-gates. Subsequently in step II, the variational parameters minimizing E_v are used in the circuit in (c), which allows to estimate the overlap betweeen the ansatz state and the variational ground state (see main text and Methods). Together with the circuit b we perform a VQE calculation to obtain the first excited state energy E_m (step III, triangles). In the final step IV, we compute the energy difference M_m = E_m − E_v and obtain the mass of the meson, shown in panel d. In all panels, solid or dashed lines correspond to results derived via exact diagonalisation, error bars for experimental data are hidden due to the marker size (see “Methods” for a more detailed discussion).

Fig. 5. Mass ratio of lightest SU(2) meson and baryon in parameter space.

a Displays lines of constant mass ratios r in the $\left(x,\tilde{m}\right)$ plane obtained from exact diagonalisation for lattices of size N = 2, 4, 6. The blue horizontal line marks the cut shown in (b). For N = 2 we supply the experimental VQE results for the meson mass with data obtained via exact diagonalisation of the baryon energy, which is trivial for this lattice size. For N = 4 the meson energy is obtained via a classical calculation of a VQE including statistical errors, using the same measurement protocol as in the experimental run. Most of the error bars are hidden by the markers, see “Methods” for a more detailed discussion.

Fig. 6. Classical simulation of a VQE to estimate the baryon mass for N = 6.

For different values of $\tilde{m}$ we calculate the mass either via an exact diagonalisation (solid lines) or with the magnetisation preserving VQE ansatz in equation (13) (boxes). The case N = 4 and $\tilde{m}=1$ calculated on real quantum hardware is shown in Fig. 3 of the main text.

Fig. 7. General baryon circuit for N = 4.

The parametric part of the circuit involves nine variational parameters (θ₁, θ₂, …, θ₉), while the static part can be incorporated into the Hamiltonian to reduce the computational effort as discussed in the main text. The colored gates mark (controlled) rotations around the y-axis with the angle of rotation indicated. White control marks denote the active application of the gate when the control is in $∣\downarrow ⟩$. The circuit, when applied to the initial state $∣\uparrow \uparrow \uparrow \uparrow \uparrow \uparrow \uparrow \uparrow ⟩$, generates the 16 basis states satisfying the B = 1 symmetry (reported in Table 1) and combines them to form color singlet thus reducing the total number of necessary variational parameters. Classical simulations of noiseless VQE using this circuit have demonstrated a high fidelity with the exact ground state in the B = 1 sector.