Skip to main page content
U.S. flag

An official website of the United States government

Dot gov

The .gov means it’s official.
Federal government websites often end in .gov or .mil. Before sharing sensitive information, make sure you’re on a federal government site.

Https

The site is secure.
The https:// ensures that you are connecting to the official website and that any information you provide is encrypted and transmitted securely.

Access keys NCBI Homepage MyNCBI Homepage Main Content Main Navigation
. 2021 Nov 12;16(11):e0259266.
doi: 10.1371/journal.pone.0259266. eCollection 2021.

Adaptive kernel fuzzy clustering for missing data

Anny K G Rodrigues  1 , Raydonal Ospina  1 , Marcelo R P Ferreira  2
Affiliations

Adaptive kernel fuzzy clustering for missing data

Anny K G Rodrigues et al. PLoS One. .

Abstract

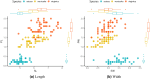
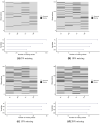
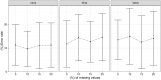
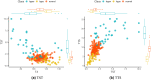
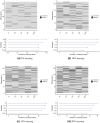
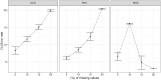
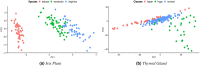
Many machine learning procedures, including clustering analysis are often affected by missing values. This work aims to propose and evaluate a Kernel Fuzzy C-means clustering algorithm considering the kernelization of the metric with local adaptive distances (VKFCM-K-LP) under three types of strategies to deal with missing data. The first strategy, called Whole Data Strategy (WDS), performs clustering only on the complete part of the dataset, i.e. it discards all instances with missing data. The second approach uses the Partial Distance Strategy (PDS), in which partial distances are computed among all available resources and then re-scaled by the reciprocal of the proportion of observed values. The third technique, called Optimal Completion Strategy (OCS), computes missing values iteratively as auxiliary variables in the optimization of a suitable objective function. The clustering results were evaluated according to different metrics. The best performance of the clustering algorithm was achieved under the PDS and OCS strategies. Under the OCS approach, new datasets were derive and the missing values were estimated dynamically in the optimization process. The results of clustering under the OCS strategy also presented a superior performance when compared to the resulting clusters obtained by applying the VKFCM-K-LP algorithm on a version where missing values are previously imputed by the mean or the median of the observed values.

PubMed Disclaimer

Conflict of interest statement

The authors have declared that no competing interests exist.

Figures

Fig 1
Fig 1. Types of missing data patterns.
(a) Multivariate. (b) Monotone. (C) General. (d) File-matching.
Fig 2
Fig 2. Scatter plots and boxplots for the Iris Plant dataset.
(a) Length. (b) Width.
Fig 3
Fig 3. Visualizations of the patterns and frequencies of the missing values by variable for the Iris Plant dataset.
(a) 5% missing. (b) 10% missing. (c) 15% missing. (d) 20% missing.
Fig 4
Fig 4. Average error rates after 100 repetitions for the Iris Plant dataset.
Fig 5
Fig 5. Scatter plots and boxplots for the Thyroid Gland dataset.
(a) TST. (b) TTS.
Fig 6
Fig 6. Graphs of missing value patterns and frequencies per variable for the Thyroid Gland dataset.
(a) 5% missing. (b) 10% missing. (c) 15% missing. (d) 20% missing.
Fig 7
Fig 7. Average results of 100 repetitions for the error rate with Thyroid Gland dataset.
Fig 8
Fig 8. Performance graphs of the methods for different percentages of missing values.
(a) Iris Plant. (b) Thyroid Gland.
Fig 9
Fig 9. Principal component analysis applied to both datasets.
(a) Iris Plant. (b) Thyroid Gland.
Fig 10
Fig 10. Scatter plots and boxplots for the Thyroid Gland dataset considering the different imputation methods.
(a) Imputation via OCS with 5% of missing values. (b) Mean imputation with 5% of missing values. (c) Median imputation with 5% of missing values. (d) Imputation via OCS with 15% of missing values. (e) Mean imputation with 15% of missing values. (f) Median imputation with 5% of missing values.
See this image and copyright information in PMC

Similar articles

See all similar articles

References

    1. Estivill-Castro V. Why so many clustering algorithms: a position paper. SIGKDD explorations. 2002;4(1):65–75. doi: 10.1145/568574.568575 - DOI
    1. Shen H, Yang J, Wang S, Liu X. Attribute weighted mercer kernel based fuzzy clustering algorithm for general non-spherical datasets. Soft Computing. 2006;10(11):1061–1073. doi: 10.1007/s00500-005-0043-5 - DOI
    1. Jain AK, Murty MN, Flynn PJ. Data clustering: a review. ACM computing surveys (CSUR). 1999;31(3):264–323. doi: 10.1145/331499.331504 - DOI
    1. Xu R, Donald Wunsch I. Survey of Clustering Algorithms. IEEE TRANSACTIONS ON NEURAL NETWORKS. 2005;16(3):645. doi: 10.1109/TNN.2005.845141 - DOI - PubMed
    1. Filippone M, Camastra F, Masulli F, Rovetta S. A survey of kernel and spectral methods for clustering. Pattern recognition. 2008;41(1):176–190. doi: 10.1016/j.patcog.2007.05.018 - DOI