A Self-Calibration Stitching Method for Pitch Deviation Evaluation of a Long-Range Linear Scale by Using a Fizeau Interferometer

Abstract

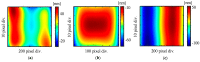
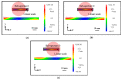
An interferometric self-calibration method for the evaluation of the pitch deviation of scale grating has been extended to evaluate the pitch deviation of the long-range type linear scale by utilizing the stitching interferometry technique. Following the previous work, in which the interferometric self-calibration method was proposed to assess the pitch deviation of the scale grating by combing the first-order diffracted beams from the grating, a stitching calibration method is proposed to enlarge the measurement range. Theoretical analysis is performed to realize the X-directional pitch deviation calibration of the long-range linear scale while reducing the second-order accumulation effect by canceling the influence of the reference flat error in the sub-apertures' measurements. In this paper, the stitching interferometry theory is briefly reviewed, and theoretical equations of the X-directional pitch deviation stitching are derived for evaluation of the pitch deviation of the long-range linear scale. Followed by the simulation verification, some experiments with a linear scale of 105 mm length from a commercial interferential scanning-type optical encoder are conducted to verify the feasibility of the self-calibration stitching method for the calibration of the X-directional pitch deviation of the linear scale over its whole area.

Keywords: linear scale; optical encoder; pitch deviation; self-calibration; stitching interferometry.

Figure 1

Schematic of the concept of the Z-directional surface form stitching interferometry and the influence of calibration error on stitching result.

Figure 2

Measurement of the positive first-order diffracted beams from the grating by using the Littrow setup.

Figure 3

Schematic of the phase error generated by the X-directional pitch deviation in stitching measurement.

Figure 4

Flow diagram indicating the working principle and the data flow of the stitching algorithm for the calibration of the long-range linear scale pitch deviation.

Figure 5

Simulation results of the form errors of a linear scale. (a) Out-of-flatness error; (b) Reference flat error; (c) X-directional pitch deviation.

Figure 6

Simulation results of the positive and negative first-order diffracted beams. (a) Sub-apertures of the positive first-order diffracted beams; (b) Sub-apertures of the negative first-order diffracted beams.

Figure 7

Simulated reference flat error for each sub-aperture.

Figure 8

Reconstructed pitch deviation results using the stitched first-order diffracted beams and the pitch deviation maps. (a) Evaluated pitch deviation obtained by using the stitched first-order diffracted beams; (b) Evaluated pitch deviation obtained by directly stitching the pitch deviation maps; (c) Difference obtained from the two results (a,b); (d) Difference between the evaluated pitch deviation and the simulated pitch deviation in Figure 5c.

Figure 9

Experimental setup with a commercial Fizeau interferometer.

Figure 10

Measured positive first-order diffracted wavefront from the linear scale grating. (a) X-directional positive first-order diffracted beam from Sub-aperture 1; (b) X-directional positive first-order diffracted beam from Sub-aperture 2; (c) X-directional positive first-order diffracted beam from Sub-aperture 3.

Figure 11

Measured negative first-order diffracted wavefront from the linear scale grating. (a) X-directional negative first-order diffracted beam from Sub-aperture 1; (b) X-directional negative first-order diffracted beam from Sub-aperture 2; (c) X-directional negative first-order diffracted beam from Sub-aperture 3.

Figure 12

Evaluated X-directional pitch deviation of the linear scale through different stitching strategies. (a) Pitched deviation evaluated from stitched first-order diffracted beams; (b) Pitched deviation evaluated by stitching the pitch deviation from each sub-aperture; (c) Difference obtained from the two results in (a,b).

Figure 13

Measured first-order diffracted beams from the linear scale with one-shot measurement. (a) X-directional positive first-order diffracted beam; (b) X-directional negative first-order diffracted beam.

Figure 14

Evaluated pitch deviation of the linear scale through one-shot and three-shot measurements. (a) Pitch deviation of the linear scale evaluated with a one-shot measurement; (b) Pitch deviation of the linear scale evaluated with a three-shot measurement and stitching method.

Figure 15

Comparison of the X-directional averaged cross-sections of the measured and stitched pitch deviation through one-shot and three-shot measurements. (a) X-directional averaged cross-section of the measured and stitched pitch deviation results; (b) Reconstruction results of the two averaged pitch deviation cross-sections and their difference.