Channels with Helical Modulation Display Stereospecific Sensitivity for Chiral Superstructures

Abstract

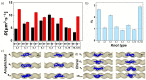
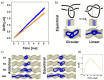
By means of coarse-grained molecular dynamics simulations, we explore chiral sensitivity of confining spaces modelled as helical channels to chiral superstructures represented by polymer knots. The simulations show that helical channels exhibit stereosensitivity to chiral knots localized on linear chains by effect of external pulling force and also to knots embedded on circular chains. The magnitude of the stereoselective effect is stronger for torus knots, the effect is weaker in the case of twist knots, and amphichiral knots do exhibit no chiral effects. The magnitude of the effect can be tuned by the so-far investigated radius of the helix, the pitch of the helix and the strength of the pulling force. The model is aimed to simulate and address a range of practical situations that may occur in experimental settings such as designing of nanotechnological devices for the detection of topological state of molecules, preparation of new gels with tailor made stereoselective properties, or diffusion of knotted DNA in biological conditions.

Keywords: DNA; chirality; coarse-grained simulations; confinement; knot; molecular dynamics; nanochannel; nanotechnology; polymer; topology.

Figure 1

Drift analysis of knots along polymer chain from molecular trajectories. (a) The figure shows the distance Δx travelled by the drifting knot as a function of time. A snapshot from the simulation shows the shape and localization of a trefoil knot, <+>3₁. The graph in the middle shows the instantaneous position of the knot along the polymer, x. The sawtooth pattern emerges from the changes of the direction of external pulling force. The bottom graph shows the periods of pulling with positive or negative force F_ext = 0.05 ε₀/σ = 0.07 pN oriented along the x-axis. (b) The graph shows drifted distance for selected knots (<+>3₁, <−>3₁ and 4₁) with linear fits (red lines) with the slope corresponding to the drift speed. A snapshot from the simulation shows the shape and localization of the achiral 4₁ twist knot. (c) The panel shows ballistic behavior of mean square displacement (MSD) typical for movement of particles in the presence of external force fitted by quadratic equation (0.05 × Dt/σ)² + 2Dt (shown as red lines) in order to obtain diffusivities.

Figure 2

Trefoil knot in helical confinement. (a) A snapshot of trefoil with positive writhe <+>3₁ in a channel with negatively oriented helicity representing an antichiral configuration. The blue circles indicate start and end bead of the knot detected by KymoKnot and Knoto-ID, the green circle indicates the middle bead of the knot, and the red circle is the center of mass of the knot. The yellow arrows indicate the direction of external pulling force for the particular snapshot. (b) Equichiral system of a trefoil with a negative writhe <−>3₁ in a channel with negative helicity (c,d) distribution of the knot starts and ends middle points and center of masses of the knot. (e) Global radius of curvature (GRC) ρ_G compared to radius of the channel R_ch = 1.5 σ along the size of the knot; in the insets, the GRC is shown in green transparent color. (f) Total drift of the knot Δx along the polymer as a function of time compared for the equichiral and antichiral systems.

Figure 3

Effect of radius of the helix R_H on dynamic and geometrical properties. (a) Speed of self-reptation of righthanded <−>3₁ and lefthanded knots <+>3₁ placed in negatively wound helical channel (ω-) representing equichiral and antichiral system; dashed line corresponds to effective diffusivity predicted for a given tortuosity D_eff = D₀/τ = D₀L/C. (b) Snapshot of trefoils in helical channels for different radii of helix indicated by numbers. (c–f) Dependence of geometrical descriptors gyration radius, R_g, knot length, L_k, asphericity, A, and prolateness, P, with the radius of the helix.

Figure 4

Stereoselectivity of the helical channel as a function of three parameters. (a) Effect of the radius of the helical channel on stereoselectivity of the channel in terms of φ_D = D₌/D_±. (b) Effect of the external pulling force F_ext. (c) Effect of the distance between of the loops or steepness of the helical channel in terms of its pitch, k. (d) Snapshots from the simulations with varying external force, the values F_extσ/ε₀ are indicated as numbers, for antichiral and equichiral configurations and channels with R_H = 1σ. (e) The channels with various pitch parameters, k, indicated as numbers to the left in helical channels with R_H = 1σ. The lines are provided as visual guides.

Figure 5

Stereoselectivity of helical channels (R_H = 1σ) for different knot types. (a) Diffusivities of grouped enantiomers of different knot types in helical confinement. For amphichiral knots (4₁, 6₃ and 8₁₈), we flipped handedness of the channel rather than writhe of the knot. (b) Magnitude of the stereoselectivity of the helical channel expressed as φ_D = D₌/D_±. The dashed line indicates no selectivity. (c) Snapshots from simulations showing the situation of the knotted portions in helical channels for amphichiral system with righthanded (left) and lefthanded helical channel (right). (d) Snapshots from simulations showing the situation of the knotted portions in helical channels for chiral knots, with equichiral (left) and antichiral (right) placement of knots in righthanded helical channel. The handedness of the channels is indicated by ω+ and ω−.

Figure 6

Stereoselectivity of helical channel (R_H = 1σ) on trefoil embedded on a circular chain. (a) Total drift over the time for antichiral and equichiral system shown for 5 overlapped trajectories for each setting. (b) Difference between orientation of the plane of the righthanded knot’s arc that is responsible for friction with the walls of the helical channel and stereoselective effect. (c) Snapshots from the molecular dynamics simulations showing circular chains with different handedness and also different lengths of the polymer indicated by number. (d) Relative difference between drift speeds in antichiral versus equichiral systems D_±/D₌.