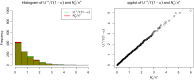
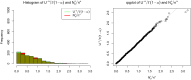
Taylor's law of fluctuation scaling for semivariances and higher moments of heavy-tailed data

Abstract

We generalize Taylor's law for the variance of light-tailed distributions to many sample statistics of heavy-tailed distributions with tail index α in (0, 1), which have infinite mean. We show that, as the sample size increases, the sample upper and lower semivariances, the sample higher moments, the skewness, and the kurtosis of a random sample from such a law increase asymptotically in direct proportion to a power of the sample mean. Specifically, the lower sample semivariance asymptotically scales in proportion to the sample mean raised to the power 2, while the upper sample semivariance asymptotically scales in proportion to the sample mean raised to the power [Formula: see text] The local upper sample semivariance (counting only observations that exceed the sample mean) asymptotically scales in proportion to the sample mean raised to the power [Formula: see text] These and additional scaling laws characterize the asymptotic behavior of commonly used measures of the risk-adjusted performance of investments, such as the Sortino ratio, the Sharpe ratio, the Omega index, the upside potential ratio, and the Farinelli-Tibiletti ratio, when returns follow a heavy-tailed nonnegative distribution. Such power-law scaling relationships are known in ecology as Taylor's law and in physics as fluctuation scaling. We find the asymptotic distribution and moments of the number of observations exceeding the sample mean. We propose estimators of α based on these scaling laws and the number of observations exceeding the sample mean and compare these estimators with some prior estimators of α.

Keywords: Pareto; Taylor’s law; power law; semivariance; stable law.

Fig. 1

Histogram and quantile–quantile plot of $N_n^{+}/n^{\alpha }$ and $U^{-\alpha }/\mathrm{\Gamma }(1-\alpha )$ for $\alpha =0.25$. The P value of the KS test is 0.1995.

Fig. 2

Histogram and quantile–quantile plot of $N_n^{+}/n^{\alpha }$ and $U^{-\alpha }/\mathrm{\Gamma }(1-\alpha )$ for $\alpha =0.50$. The P value of the KS test is 0.9135.