A model for learning based on the joint estimation of stochasticity and volatility
- PMID: 34782597
- PMCID: PMC8592992
- DOI: 10.1038/s41467-021-26731-9
A model for learning based on the joint estimation of stochasticity and volatility
Abstract
Previous research has stressed the importance of uncertainty for controlling the speed of learning, and how such control depends on the learner inferring the noise properties of the environment, especially volatility: the speed of change. However, learning rates are jointly determined by the comparison between volatility and a second factor, moment-to-moment stochasticity. Yet much previous research has focused on simplified cases corresponding to estimation of either factor alone. Here, we introduce a learning model, in which both factors are learned simultaneously from experience, and use the model to simulate human and animal data across many seemingly disparate neuroscientific and behavioral phenomena. By considering the full problem of joint estimation, we highlight a set of previously unappreciated issues, arising from the mutual interdependence of inference about volatility and stochasticity. This interdependence complicates and enriches the interpretation of previous results, such as pathological learning in individuals with anxiety and following amygdala damage.
© 2021. The Author(s).
Conflict of interest statement
The authors declare no competing interests.
Figures
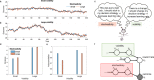
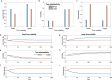
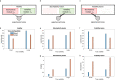
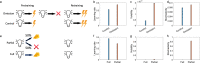


Similar articles
-
Computational processes of simultaneous learning of stochasticity and volatility in humans.Nat Commun. 2024 Oct 21;15(1):9073. doi: 10.1038/s41467-024-53459-z. Nat Commun. 2024. PMID: 39433765 Free PMC article.
-
State anxiety biases estimates of uncertainty and impairs reward learning in volatile environments.Neuroimage. 2021 Jan 1;224:117424. doi: 10.1016/j.neuroimage.2020.117424. Epub 2020 Oct 6. Neuroimage. 2021. PMID: 33035670
-
Stochastic decisions support optimal foraging of volatile environments, and are disrupted by anxiety.Cogn Affect Behav Neurosci. 2025 Jun;25(3):868-885. doi: 10.3758/s13415-024-01256-y. Epub 2025 Jan 9. Cogn Affect Behav Neurosci. 2025. PMID: 39789398 Free PMC article.
-
Expecting the unexpected: a review of learning under uncertainty across development.Cogn Affect Behav Neurosci. 2023 Jun;23(3):718-738. doi: 10.3758/s13415-023-01098-0. Epub 2023 May 26. Cogn Affect Behav Neurosci. 2023. PMID: 37237092 Free PMC article. Review.
-
Adaptive learning under expected and unexpected uncertainty.Nat Rev Neurosci. 2019 Oct;20(10):635-644. doi: 10.1038/s41583-019-0180-y. Nat Rev Neurosci. 2019. PMID: 31147631 Free PMC article. Review.
Cited by
-
Dynamical self-organization and efficient representation of space by grid cells.Curr Opin Neurobiol. 2021 Oct;70:206-213. doi: 10.1016/j.conb.2021.11.007. Epub 2021 Nov 30. Curr Opin Neurobiol. 2021. PMID: 34861597 Free PMC article. Review.
-
Dynamic prefrontal coupling coordinates adaptive decision-making.Res Sq [Preprint]. 2025 Apr 9:rs.3.rs-6296852. doi: 10.21203/rs.3.rs-6296852/v1. Res Sq. 2025. PMID: 40297698 Free PMC article. Preprint.
-
Blocked training facilitates learning of multiple schemas.Commun Psychol. 2024 Apr 9;2(1):28. doi: 10.1038/s44271-024-00079-4. Commun Psychol. 2024. PMID: 39242783 Free PMC article.
-
Uncertainty alters the balance between incremental learning and episodic memory.Elife. 2022 Dec 2;11:e81679. doi: 10.7554/eLife.81679. Elife. 2022. PMID: 36458809 Free PMC article.
-
Specifying the timescale of early life unpredictability helps explain the development of internalising and externalising behaviours.Sci Rep. 2024 Feb 12;14(1):3563. doi: 10.1038/s41598-024-54093-x. Sci Rep. 2024. PMID: 38347055 Free PMC article.
References
-
- Dayan, P. & Long, T. Statistical Models of Conditioning. In Advances in Neural Information Processing Systems 10 (eds, Jordan, M., Kearns, M. & Solla, S.) 117–123 (MIT Press, 1998).
-
- Dayan P, Kakade S, Montague PR. Learning and selective attention. Nat. Neurosci. 2000;3:1218–1223. - PubMed
-
- Courville AC, Daw ND, Touretzky DS. Bayesian theories of conditioning in a changing world. Trends Cogn. Sci. (Regul. Ed.) 2006;10:294–300. - PubMed
-
- Gershman SJ, Blei DM, Niv Y. Context, learning, and extinction. Psychol. Rev. 2010;117:197–209. - PubMed
Publication types
MeSH terms
LinkOut - more resources
Full Text Sources

