Three-dimensional loop extrusion

Abstract

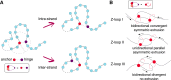
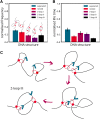
Loop extrusion convincingly describes how certain structural maintenance of chromosome (SMC) proteins mediate the formation of large DNA loops. Yet most of the existing computational models cannot reconcile recent in vitro observations showing that condensins can traverse each other, bypass large roadblocks, and perform steps longer than their own size. To fill this gap, we propose a three-dimensional (3D) "trans-grabbing" model for loop extrusion, which not only reproduces the experimental features of loop extrusion by one SMC complex but also predicts the formation of so-called Z-loops via the interaction of two or more SMCs extruding along the same DNA substrate. By performing molecular dynamics simulations of this model, we discover that the experimentally observed asymmetry in the different types of Z-loops is a natural consequence of the DNA tethering in vitro. Intriguingly, our model predicts this bias to disappear in the absence of tethering and a third type of Z-loop, which has not yet been identified in experiments, to appear. Our model naturally explains roadblock bypassing and the appearance of steps larger than the SMC size as a consequence of non-contiguous DNA grabbing. Finally, this study is the first, to our knowledge, to address how Z-loops and bypassing might occur in a way that is broadly consistent with existing cis-only 1D loop extrusion models.

Figure 1

A three-dimensional (3D) or “trans-grabbing” model for loop extrusion. (A) We model LEFs as springs connecting two polymer beads; one of these beads is denoted as the “anchor” that does not move while the other is denoted as the “hinge” that can jump to 3D proximal but non-contiguous polymer segments. By updating the position of the hinge via a mix of intra- and interstrand moves, the system is driven to form Z-loops. (B) We identify three types of Z-loops: Z-loop I ($Z_I$) has both hinges pointing outward, thus yielding symmetric extrusion; Z-loop II ($Z_{II}$) has both hinges pointing in the same direction and thus yields asymmetric extrusion; finally, Z-loop III ($Z_{III}$) has both hinges pointing inward and displays no net extrusion. Only $Z_I$ and $Z_{II}$ were observed in experiments (40).

Figure 2

Implementation of 3D extrusion. A LEF is modeled as a spring connecting two non-contiguous beads and with rest length $r_0=1.6\sigma$. Every 8000 simulations steps ($\simeq 0.01$ s), we attempt to move the LEF by gathering the 3D neighbors within a Euclidean distance $r_G=3.4\sigma$ from the anchor. Of these, the ones that fall within the $d_C=5$ nearest neighbors are classified as 1D beads. A random bead from the list of 3D “trans” neighbors is selected with probability $p_{inter}=5\times {10}^{-3}$ (in supporting material we show results with a different choice of this parameter) and a random bead from the 1D list otherwise. Finally, we update the beads connected by the spring and evolve the equations of motion of the beads so that the spring relaxes to its equilibrium rest length $r_0$. We note that setting $p_{inter}=0$ and $d_C=2$ maps back to the standard cis-only loop extrusion model (19, 21).

Figure 3

(A) MD simulations of doubly tethered DNA (cyan) loaded with one asymmetric LEF (violet and red) extruding a loop (blue). (B) Mean relative DNA extension as a function of time. The relative extension is defined as the end-to-end distance divided by the difference between the total length of the DNA and the length of the extruded loop. (C) Extrusion rate as a function of time. (D) Extrusion rate as a function of tension: comparison between our simulations (dark-gray squares) and experimental data from (5) (cyan “+”).

Figure 4

(A–E) A summary of the five Z-loop topologies observed in simulations with two LEFs (the anchored bead “a” and the moving hinge “h”): (A) separated; (B) nested; (C) Z-loop I (this structure grows as DNA is reeled in from the outward-facing hinges); (D) Z-loop II (only one of the boundaries moves with respect to the structure); (E) Z-loop III (both boundaries of the structure are fixed as the anchors are facing inward). See also Fig. S5 in the supporting material for a stepwie scheme on the formation of these loop topologies. (F and G) Schematic illustration of the initial configuration of MD simulations with two nested LEFs. When the second LEF is loaded, its extrusion direction either opposes (F) or copies (G) the extrusion direction of the first one. Blue arrows indicate in which direction DNA is reeled inside a loop. (H and I) MD simulations of doubly tethered DNA loaded with two LEFs. (H) When the LEFs are nested, one of the loops (gray) extruded by the two protein complexes is part of the other loop (gray + blue). (I) Two condensins can fold a Z-loop (type I in the figure). One of the three segments (gray) involved in a Z-loop is shared between the loops extruded by the two condensins (gray + blue and gray + lilac). (J and K) Frequency (J) and survival times (K) of topological structures in simulations of two nested LEFs on doubly tethered DNA.

Figure 5

Asymmetry in the frequency of $Z_I$ and $Z_{II}$ on DNA with two tethered ends. (A) At each extrusion step, the segment of DNA (cream) on the intake side is likely to be pulled taut and roughly parallel to the line connecting the two ends of the tethered DNA. The anchor-side part is instead relaxed as no tension is applied. (B) This effective alignment biases the extruded loop to fold over the anchor side of the most external LEF. In turn, this favors the nested LEF to grab segments of DNA from over the anchor side (b) rather than over the hinge side (a) (see Fig. 3A). (C) (i) If the two nested LEFs are extruding in the same direction and the internal LEF, labeled a, approaches the other one (b), a $Z_{II}$ is formed when a's hinge jumps other b's hinge. When the jump is attempted, however, b's hinge is running away from a's hinge. (ii) If instead the LEFs are extruding in opposite directions, a $Z_I$ is formed when a's hinge jumps the other b's anchor, which does not move. Move (ii) (yielding $Z_I$) is more likely to succeed due to the slower dynamics of the polymer near an LEF anchor.

Figure 6

Results of simulations of nested LEFs on singly tethered DNA. (A, C, and E) Frequency of topologies folded by two LEFs loaded with the same (A) or opposite (C) initial directions. (B, D, and F) Mean normalized lifetime of the loop topologies.

Figure 7

(A and B) Results of simulations of two initially separated LEFs loaded on doubly tethered DNA with opposite initial extrusion directions. Frequency (A) and mean normalized lifetime (B) of the topologies. (C) Scheme of the formation of a $Z_{III}$ in simulations with two initially separated LEFs and opposite extrusion directions. $Z_{III}$ is formed if one of the hinges jumps over the other.