Improvement of the Gaussian Electrostatic Model by separate fitting of Coulomb and exchange-repulsion densities and implementation of a new dispersion term
- PMID: 34800949
- PMCID: PMC8598263
- DOI: 10.1063/5.0072380
Improvement of the Gaussian Electrostatic Model by separate fitting of Coulomb and exchange-repulsion densities and implementation of a new dispersion term
Abstract
The description of each separable contribution of the intermolecular interaction is a useful approach to develop polarizable force fields (polFFs). The Gaussian Electrostatic Model (GEM) is based on this approach, coupled with the use of density fitting techniques. In this work, we present the implementation and testing of two improvements of GEM: the Coulomb and exchange-repulsion energies are now computed with separate frozen molecular densities and a new dispersion formulation inspired by the Sum of Interactions Between Fragments Ab initio Computed polFF, which has been implemented to describe the dispersion and charge-transfer interactions. Thanks to the combination of GEM characteristics and these new features, we demonstrate a better agreement of the computed structural and condensed properties for water with experimental results, as well as binding energies in the gas phase with the ab initio reference compared with the previous GEM* potential. This work provides further improvements to GEM and the items that remain to be improved and the importance of the accurate reproduction for each separate contribution.
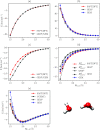
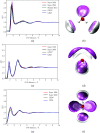
Figures





Similar articles
-
S/G-1: an ab initio force-field blending frozen Hermite Gaussian densities and distributed multipoles. Proof of concept and first applications to metal cations.J Phys Chem A. 2014 Sep 4;118(35):7598-612. doi: 10.1021/jp5051657. Epub 2014 Jun 19. J Phys Chem A. 2014. PMID: 24878003
-
Towards a force field based on density fitting.J Chem Phys. 2006 Mar 14;124(10):104101. doi: 10.1063/1.2173256. J Chem Phys. 2006. PMID: 16542062 Free PMC article.
-
QM/MM Simulations with the Gaussian Electrostatic Model: A Density-based Polarizable Potential.J Phys Chem Lett. 2018 Jun 7;9(11):3062-3067. doi: 10.1021/acs.jpclett.8b01412. Epub 2018 May 23. J Phys Chem Lett. 2018. PMID: 29775314 Free PMC article.
-
Accurate first principles model potentials for intermolecular interactions.Annu Rev Phys Chem. 2013;64:553-78. doi: 10.1146/annurev-physchem-040412-110031. Annu Rev Phys Chem. 2013. PMID: 23561011 Review.
-
An extensive assessment of the performance of pairwise and many-body interaction potentials in reproducing ab initio benchmark binding energies for water clusters n = 2-25.Phys Chem Chem Phys. 2023 Mar 8;25(10):7120-7143. doi: 10.1039/d2cp03241d. Phys Chem Chem Phys. 2023. PMID: 36853239 Review.
Cited by
-
Performance Tuning of Polarizable Gaussian Multipole Model in Molecular Dynamics Simulations.J Chem Theory Comput. 2025 Jan 28;21(2):847-858. doi: 10.1021/acs.jctc.4c01368. Epub 2025 Jan 8. J Chem Theory Comput. 2025. PMID: 39772516 Free PMC article.
-
A Simple Electron-Density Based Force Field Model for High-Energy Interactions between Atoms and Molecules.J Phys Chem A. 2024 Feb 15;128(6):1163-1172. doi: 10.1021/acs.jpca.3c06724. Epub 2024 Feb 6. J Phys Chem A. 2024. PMID: 38320398 Free PMC article.
-
Development of the Quantum-Inspired SIBFA Many-Body Polarizable Force Field: Enabling Condensed-Phase Molecular Dynamics Simulations.J Chem Theory Comput. 2022 Jun 14;18(6):3607-3621. doi: 10.1021/acs.jctc.2c00029. Epub 2022 May 16. J Chem Theory Comput. 2022. PMID: 35575306 Free PMC article.
References
-
- Cisneros G. A., Wikfeldt K. T., Ojamäe L., Lu J., Xu Y., Torabifard H., Bartók A. P., Csányi G., Molinero V., and Paesani F., “Modeling molecular interactions in water: From pairwise to many-body potential energy functions,” Chem. Rev. 116, 7501–7528 (2016).10.1021/acs.chemrev.5b00644 - DOI - PMC - PubMed
-
- Ren P. and Ponder J. W., “Polarizable atomic multipole water model for molecular mechanics simulation,” J. Phys. Chem. B 107, 5933–5947 (2003).10.1021/jp027815+ - DOI
-
- Day P. N., Jensen J. H., Gordon M. S., Webb S. P., Stevens W. J., Krauss M., Garmer D., Basch H., and Cohen D., “An effective fragment method for modeling solvent effects in quantum mechanical calculations,” J. Chem. Phys. 105, 1968–1986 (1996).10.1063/1.472045 - DOI
Grants and funding
LinkOut - more resources
Full Text Sources
Research Materials

