On some fundamental challenges in monitoring epidemics

Abstract

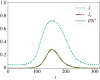
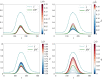
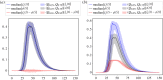
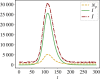
Epidemic models often reflect characteristic features of infectious spreading processes by coupled nonlinear differential equations considering different states of health (such as susceptible, infectious or recovered). This compartmental modelling approach, however, delivers an incomplete picture of the dynamics of epidemics, as it neglects stochastic and network effects, and the role of the measurement process, on which the estimation of epidemiological parameters and incidence values relies. In order to study the related issues, we combine established epidemiological spreading models with a measurement model of the testing process, considering the problems of false positives and false negatives as well as biased sampling. Studying a model-generated ground truth in conjunction with simulated observation processes (virtual measurements) allows one to gain insights into the fundamental limitations of purely data-driven methods when assessing the epidemic situation. We conclude that epidemic monitoring, simulation, and forecasting are wicked problems, as applying a conventional data-driven approach to a complex system with nonlinear dynamics, network effects and uncertainty can be misleading. Nevertheless, some of the errors can be corrected for, using scientific knowledge of the spreading dynamics and the measurement process. We conclude that such corrections should generally be part of epidemic monitoring, modelling and forecasting efforts. This article is part of the theme issue 'Data science approaches to infectious disease surveillance'.

Keywords: complex systems; computer simulation; data science; epidemic modelling; network theory; statistics.

Figure 1.

Estimation of the true proportion $I/N^{\prime }$ of Infectious (green solid line) based on the fraction (3.3) of positive tests (blue dotted line) and the correction formula (3.11) (red dashed-dotted line). The corrected estimate tends to be very close to the true value when the parameters $\alpha$, $\beta$, $p$ and $q$ of the test method are known exactly. The monitoring parameters are: $\alpha =0.05$, $\beta =0.15$, $p=0.8$, $q=0.06$. The curves displayed here are for SEIRD dynamics with $N=100\hspace{0.17em}000$, $a=1/5$, $b=3/14$, $c=1/28$, $d=1/28$. (Online version in colour.)

Figure 2.

Estimation of the true proportion $I/N^{\prime }$ of Infectious (green solid line) based on the fraction (3.3) of positive tests (blue dotted line) and the correction formula (3.11) (other lines according to the colour scales on the right). In these figures, we assume that only three of the four parameters $\alpha =0.05$, $\beta =0.15$, $p=0.8$ and $q=0.06$ are known exactly, while the estimate of the fourth one (represented with a hat on top) is uncertain and, therefore, varied. Specifically, in (3.11) we have replaced $\alpha$ by $\hat{\alpha }$ in the top left figure, $\beta$ by $\hat{\beta }$ in the top right figure, $p$ by $\hat{p}$ in the bottom left figure and $q$ by $\hat{q}$ in the bottom right figure. All figures show results for a SEIRD dynamics with $N=100\hspace{0.17em}000$, $a=1/5$, $b=3/14$, $c=1/28$, $d=1/28$. (Online version in colour.)

Figure 3.

Ensemble of stochastic trajectories (SP-KMC sampling) on an ensemble of ${10}^3$ Barabási-Albert networks with $N=100\hspace{0.17em}000$, $\mu =3$ and $\gamma =1$. (a) Accurate epidemic reconstruction assuming that the parameters $\alpha =0.05$, $\beta =0.15$, $p=0.8$, $q=0.06$ of the test method are exactly known. (b) Inaccurate reconstruction for somewhat incorrect estimates $\hat{p}=0.75$ and $\hat{q}=0.1$, while the other parameters are assumed to be the same. The assumed parameters of the SEIRD dynamics are: $a=1/5$, $b=3/14$, $c=1/28$, $d=1/28$. $Q_{0.01}$, $Q_{0.25}$, $Q_{0.75}$ and $Q_{0.99}$ represent 1, 25, 75 and 99 per cent quantiles. The median values and error quantile bands are based on ${10}^3$ simulations. (Online version in colour.)

Figure 4.

$\hat{I}(t)$ computed from (4.3), assuming uncertainty in monitoring parameters: $\hat{\alpha }\sim \mathrm{Beta}(10,90)$, $\hat{\beta }\sim \mathrm{Beta}(5,95)$, $\hat{p}\sim \mathrm{Beta}(4,16)$, $\hat{q}\sim \mathrm{Beta}(5,95)$. We used the distributions whose mean is ‘guessed’ correctly, i.e.$⟨\hat{\alpha }⟩=\alpha$. The true number $I(t)$ of Infectious was obtained by simulating SEIRD dynamics with parameters $a=1/5$, $b=3/14$, $c=1/28$, $d=1/28$ on an ER network with $N={10}^5$ and average degree $1.5$. (Online version in colour.)

Figure 5.

Posterior distribution $P(I|n_p)$ when a network topology prior is used (in red) and when it is not (in blue). Monitoring parameters were also considered as priors, with $\hat{p}\sim \mathrm{Beta}(4,16)$, $\hat{q}\sim \mathrm{Beta}(5,95)$, $\hat{\alpha }\sim \mathrm{Beta}(5,95)$, $\hat{\beta }\sim \mathrm{Beta}(10,90)$. For the ground truth parameters, we selected $\alpha =0.05$, $\beta =0.1$, $p=0.2$, $q=0.05$. The ground truth number of Infectious $I=43\hspace{0.17em}448$ was obtained from an epidemic trajectory generated on a network sampled from an ensemble of Barabási–Albert (BA) networks with $\mu =3$, $\gamma =1$, giving a scale-free network with an average degree $⟨k⟩=3$. In scenario ‘BA prior with correct $\mu =3$, $\gamma =1$’, we used a prior which assumes the correct network ensemble—Barabási-Albert networks with $N=100\hspace{0.17em}000$, $\mu =3$ and $\gamma =1$. In ‘BA prior with $\mu =6$, $\gamma =1$’, we used a network ensemble prior of BA networks with $\mu =6$ and $\gamma =1$, which over-estimates the average node degree $⟨k⟩$. In ‘BA prior with $\mu =3$, $\gamma =2$’, we used a prior for BA networks with $\mu =3$ and $\gamma =2$, and in ‘ER prior with $\pi =3\times {10}^{-5}$’ we used a prior for Erdös–Rényi networks with $\pi =3\times {10}^{-5}$, giving networks with $⟨k⟩=3$, but the degree distribution $P(k)$ is Poisson rather than a power law. In all figures, the green line shows the ‘ground truth’, against which the biased testing is performed. We observe that knowledge about the degree distribution of contacts helps to estimate the true ground truth. To estimate network priors within $t\in [60,65]$, we have used $1000$ networks from the ensemble. In all cases, $M=1000$ Monte Carlo samples were used to estimate (4.3). (Online version in colour.)