Correlated diffusion in lipid bilayers

Abstract

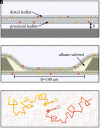
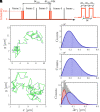
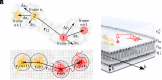
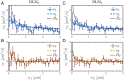
Lipid membranes are complex quasi-two-dimensional fluids, whose importance in biology and unique physical/materials properties have made them a major target for biophysical research. Recent single-molecule tracking experiments in membranes have caused some controversy, calling the venerable Saffman-Delbrück model into question and suggesting that, perhaps, current understanding of membrane hydrodynamics is imperfect. However, single-molecule tracking is not well suited to resolving the details of hydrodynamic flows; observations involving correlations between multiple molecules are superior for this purpose. Here dual-color molecular tracking with submillisecond time resolution and submicron spatial resolution is employed to reveal correlations in the Brownian motion of pairs of fluorescently labeled lipids in membranes. These correlations extend hundreds of nanometers in freely floating bilayers (black lipid membranes) but are severely suppressed in supported lipid bilayers. The measurements are consistent with hydrodynamic predictions based on an extended Saffman-Delbrück theory that explicitly accounts for the two-leaflet bilayer structure of lipid membranes.

Keywords: Saffman–Delbrück model; membrane hydrodynamics; single-molecule tracking.

Fig. 1.

Model lipid bilayer systems used to study correlated Brownian motion. (Cartoons not to scale.) The labeled probes for SPT are shown in orange and red. (A) SLB formed on a microscope cover glass. The height of the membrane above the solid support, h, is ∼1 nm. (B) BLM formed on a μm-sized aperture. (C) Probe trajectories for a pair of labeled lipids. The arrows indicate correlated motion of the probes.

Fig. 2.

Measuring and analyzing lipid motion. (A) The illumination pulsing scheme consists of pairs of laser pulses grouped around every second dead time period between camera frames. This leads to short displacement times $\mathrm{\Delta }{t}_{\mathit{short}}$ alternating with long ones $\mathrm{\Delta }{t}_{\mathit{long}}$. Motion was analyzed based exclusively on $\mathrm{\Delta }t\equiv \mathrm{\Delta }{t}_{\mathit{short}}$. (B) Zoom in on a pair of laser pulses of length $\mathrm{\Delta }{t}_{on}$ separated by a dark time of length $\mathrm{\Delta }{t}_{\mathit{off}}$. $\mathrm{\Delta }{t}_{on}$ is the time window over which lipid positions ${\mathit{r}}_{\ell }(t)$ are measured, and $\mathrm{\Delta }t=\mathrm{\Delta }{t}_{on}+\mathrm{\Delta }{t}_{\mathit{off}}$ is the interval over which lipid displacements are inferred as the difference between two successive position measurements. (C) Sample trajectory ${\mathit{r}}_2(t)$ of an Atto550-DMPE probe in BLM_h, obtained using illumination pulsing. The displacements based on $\mathrm{\Delta }t$ are shown in blue. (D) Same as C but for the SLB case. (E) Distribution of scalar displacements $\mathrm{\Delta }{r}_2$ based on $\mathrm{\Delta }t$ in BLM_h. (F) Same as E but for BLM_d. (G) Same as E but for an SLB. Gray shows full distribution, and red and blue show slow and fast populations, respectively, obtained from a two-state HMM analysis of the trajectories. Continuous lines are fits.

Fig. 3.

Correlated Brownian motion in lipid bilayers. (A) Lipid motion in the coordinate system where the x axis is defined by the vector connecting the lipid pair ${\mathit{r}}_{12}$. The probes $\ell =1,2$ move with displacements $\mathrm{\Delta }{\mathit{r}}_{\ell }=\left[\mathrm{\Delta }{x}_{\ell },\mathrm{\Delta }{y}_{\ell }\right]$ during the time interval $\mathrm{\Delta }t$. (B) Random trajectories of the probes showing the positions sampled during the finite illumination times $\mathrm{\Delta }{t}_{on}$ (indicated by the circles). The experimental detection only reveals the center of mass positions ${\mathit{r}}_{\ell }(t)$ (indicated by the crosses). It is these averaged positions that are registered experimentally to create the trajectories. (C) Bilayer model used in the RS calculations. The parameters entering the model are the distance of the membrane to the support $\mathit{h}$, the surface viscosity for a leaflet ${\mathit{\eta }}_{\mathit{m}}$, the fluid viscosity of the aqueous superphase (subphase) ${\mathit{\eta }}_{\mathit{f}}^{\pm }$, and the interleaflet friction coefficient $\mathit{b}$.

Fig. 4.

Correlated Brownian motion as a function of distance $r_{12}$ for BLMs and comparison with hydrodynamic theory. The panels show the experimental correlation functions, $c_L$ or $c_T$ (continuous line with error bars), as well as coupling diffusion coefficients calculated using the hydrodynamic theory, $D_L$ or $D_T$ (black dotted line), and the corresponding time-averaged forms, $s_L$ or $s_T$ (bold, colored dotted line). (A and B) BLM_d. (C and D) BLM_h.

Fig. 5.

Correlated Brownian motion as a function of distance $r_{12}$ for an SLB and comparison with hydrodynamic theory. Each panel shows experimental correlations, $c_L^{\alpha }$ or $c_T^{\alpha }$ (continuous line with error bars), as well as the coupling diffusion coefficients calculated using hydrodynamic theory, $D_L^{\alpha }$ or $D_T^{\alpha }$ (black dotted line), and the corresponding time-averaged forms, $s_L^{\alpha }$ or $s_T^{\alpha }$ (colored dotted line), respectively. (A and B) Distal leaflet. (C and D) Proximal leaflet. While the predicted coupling diffusion coefficients are nonzero in a very narrow window close to $r_{12}=0$, this is completely washed out by time averaging; the experiments correspondingly display no evidence of correlations.