Stress relaxation in tunable gels

Abstract

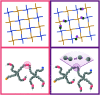
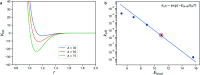
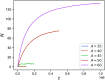
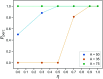
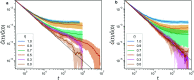
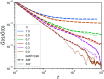
Hydrogels are a staple of biomaterials development. Optimizing their use in e.g. drug delivery or tissue engineering requires a solid understanding of how to adjust their mechanical properties. Here, we present a numerical study of a class of hydrogels made of 4-arm star polymers with a combination of covalent and reversible crosslinks. This design principle combines the flexibility and responsivity associated with reversible linkers with stability provided by chemical crosslinks. In molecular dynamics simulations of such hybrid gel networks, we observe that the strength of the reversible bonds can tune the material from solid to fluid. We identify at what fraction of reversible bonds this tunability is most pronounced, and find that the stress relaxation time of the gels in this tunable regime is set directly by the average lifetime of the reversible bonds. As our design is easy to realize in the already widely-used tetraPEG gel setting, our work will provide guidelines to improve the mechanical performance of biomedical gels.

Fig. 1. Illustration of covalent (left) and hybrid (right) tetraPEG networks. The blue and yellow star polymers represent the two complementary types of end-functionalizations. In the hybrid gel model, we replace a fraction of the covalent bonds with reversible linkers. The bottom half of the graphic shows the coarse grained model employed in our simulations.

Fig. 2. Probability P_perc of finding a percolating network as a function of polymer concentration C.

Fig. 3. Snapshot of the simulation box after equilibration and click gelation at concentration C = 8% with half of the covalent bonds replaced by reversible linker pairs η = 0.5. Figure produced with Ovito.

Fig. 4. (a) Total interaction potential between reversible patches, for different values of A; V_tot is potential between two attractive patches (combination of Gaussian and WCA), r is the distance between the centers of the larger beads in the reversible patches. The value shown is for the case in which the centers of the spheres and patches all line up: The potential increases if they meet at an angle, due to the resulting larger overlap of the repulsive spheres. (b) Unbinding rates k_off (1/t, inverse of the average bond lifetime) as a function of the depth E of the effective potential well between reversible beads; the circled dot corresponds to A = 50, for which the average bond lifetime is t = 5.1 × 10⁵; we see that the unbinding rate is set by exp(−E/k_BT).

Fig. 5. Reversible bond formation as a function of time, for a network with a concentration of 50% bonds for a range of A values.

Fig. 6. The probability P_perc of finding a percolating network as a function of the fraction of permanent bonds η. Lines are included as guides to the eye. We show data for three values of the reversible binding strength: For A = 35, the reversible linkers are rarely bound and the percolation behavior is identical to the case of A = 0. For A = 75, the “reversible” links are so strong that they never unbind. At intermediate strength A = 50, we observe a behavior in which the network fluctuates between percolating and non-percolating by virtue of the binding and unbinding of reversible linkers.

Fig. 7. (a) The stress relaxation modulus of hybrid gels (with A′B′ reversible beads) for a range of η. For η = 0.5 we performed a longer simulation to verify that it indeed relaxes to 0 ultimately. The dashed line indicates the 1/t-artifact resulting from the averaging procedure described in eqn (3). (b) The stress relaxation modulus for the same range of η, in a control experiment where the sticker interaction has been turned off. In both panels, the shaded area indicates the standard deviation of the full data.

Fig. 8. Comparison between the stress relaxation modulus (zoom in) of hybrid gels for two types of reversible patches, for a range of η; A′B′ in a thick dashed line, A′A′ in a thin solid line.