Towards Understanding the Interconnection between Celestial Pole Motion and Earth's Magnetic Field Using Space Geodetic Techniques

Abstract

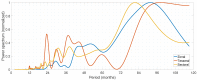
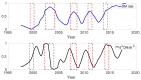
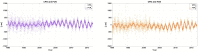
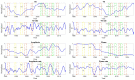
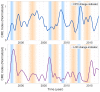
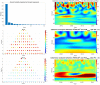
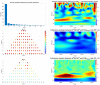
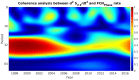
The understanding of forced temporal variations in celestial pole motion (CPM) could bring us significantly closer to meeting the accuracy goals pursued by the Global Geodetic Observing System (GGOS) of the International Association of Geodesy (IAG), i.e., 1 mm accuracy and 0.1 mm/year stability on global scales in terms of the Earth orientation parameters. Besides astronomical forcing, CPM excitation depends on the processes in the fluid core and the core-mantle boundary. The same processes are responsible for the variations in the geomagnetic field (GMF). Several investigations were conducted during the last decade to find a possible interconnection of GMF changes with the length of day (LOD) variations. However, less attention was paid to the interdependence of the GMF changes and the CPM variations. This study uses the celestial pole offsets (CPO) time series obtained from very long baseline interferometry (VLBI) observations and data such as spherical harmonic coefficients, geomagnetic jerk, and magnetic field dipole moment from a state-of-the-art geomagnetic field model to explore the correlation between them. In this study, we use wavelet coherence analysis to compute the correspondence between the two non-stationary time series in the time-frequency domain. Our preliminary results reveal interesting common features in the CPM and GMF variations, which show the potential to improve the understanding of the GMF's contribution to the Earth's rotation. Special attention is given to the corresponding signal between FCN and GMF and potential time lags between geomagnetic jerks and rotational variations.

Keywords: VLBI; celestial pole offset; geomagnetic field.

Figure 1

Multivariate spectral analysis of the second derivative of zonal, tesseral, and sectoral spherical harmonics coefficients up to degree 2.

Figure 2

Time series of dDM/dt and d²DM/dt² obtained from CHAOS6 model.

Figure 3

CPOs (dots) and FCN model $$B16$$ (line) in X (purple) and Y (orange) direction.

Figure 4

Time series of the normalized FCN offset, amplitude, and phase for the $$B16$$ model. The dashed box indicates GMJ and magnetic secular acceleration pulse (SA) at the core surface. The red color shows the confirmed GMJ. The yellow shows the questionable SA of the GMJ. The green indicates the significant global SA of the GMF.

Figure 5

Detection of the time and significance of changes in the CPO (top) and LOD (bottom) time series based on Singular Spectrum Analysis (SSA). The blue-shaded areas indicate the epochs of SA pulses and the orange-shaded areas show reported geomagnetic jerks.

Figure 6

Wavelet coherence analysis between all SHC of GMF and $$FC{N}_{Amp}$$ rate (upper panel) and the percentage of each PC. Middle left panel: SHC correlation with the first PC. Middle right panel: the coherence between GMF and $$FC{N}_{Amp}$$ rate reconstructed by PC = 1. Lower left panel: SHC correlation with the PC = 3. Lower right panel: the coherence between GMF and $$FC{N}_{Amp}$$ rate reconstructed by PC = 3. Unit of periods is month.

Figure 7

Wavelet coherence analysis between all SHC of GMF and $$FC{N}_{Phase}$$ rate (upper panel) and the percentage of each PC. Middle left panel: SHC correlation with the first PC. Middle right panel: the coherence between GMF and $$FC{N}_{Phase}$$ rate reconstructed by PC = 1. Lower left panel: SHC correlation with the PC = 2. Lower right panel: the coherence between GMF and $$FC{N}_{Phase}$$ rate reconstructed by PC = 2. Unit of periods is month.

Figure 8

Wavelet coherence analysis between $$\frac{d^2{S}_{2″}}{d{t}^2}$$ and $$FC{N}_{Phase}$$ rate.

Figure 9

Wavelet coherence between FCN (amplitude and phase) rate and DM rate.