Fractional-Order Sensing and Control: Embedding the Nonlinear Dynamics of Robot Manipulators into the Multidimensional Scaling Method

Abstract

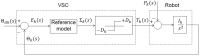
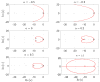
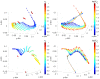
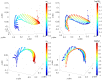
This paper studies the use of multidimensional scaling (MDS) to assess the performance of fractional-order variable structure controllers (VSCs). The test bed consisted of a revolute planar robotic manipulator. The fractional derivatives required by the VSC can be obtained either by adopting numerical real-time signal processing or by using adequate sensors exhibiting fractional dynamics. Integer (fractional) VCS and fractional (integer) sliding mode combinations with different design parameters were tested. Two performance indices based in the time and frequency domains were adopted to compare the system states. The MDS generated the loci of objects corresponding to the tested cases, and the patterns were interpreted as signatures of the system behavior. Numerical experiments illustrated the feasibility and effectiveness of the approach for assessing and visualizing VSC systems.

Keywords: fractional calculus; fractional sensor; information visualization; multidimensional scaling; robot manipulator; variable structure control.

Figure 1

Block diagram of a VSC-controlled robot link.

Figure 2

The root locus for various values of $$\alpha$$.

Figure 3

The Bode diagrams of a 6-stage fractional sensor, yielding the fractional orders: (top) $$\alpha =0.16$$; (bottom) $$\alpha =0.40$$.

Figure 4

The sensor time responses $$y_1(t$$) to the input signals $$u\left(t\right)=\left\{\delta \right(t),h(t\left)\right\}$$.

Figure 5

The 3-dim MDS locus for the IVSC-FSM, assessing the time-domain behavior, with the distances: (top) Arccosine $$d_1({\mathbf{v}}_i^{\left(t\right)},{\mathbf{v}}_j^{\left(t\right)})$$; and (bottom) Jaccard $$d_2({\mathbf{v}}_i^{\left(t\right)},{\mathbf{v}}_j^{\left(t\right)})$$. The points represent the test cases. On the left, lines connect points of constant $$\delta$$, and each color corresponds to points of constant $$\alpha$$. On the right, lines connect points of constant $$\alpha$$, and each color corresponds to points of constant $$\delta$$. The fractional order $${\alpha }_q\in [-0.5,1]$$, and the width of the band $${\delta }_q\in [{10}^{-4},{10}^1]$$.

Figure 6

The 3-dim MDS locus for the IVSC-FSM, assessing the frequency-domain behavior, with the distances: (top) Arccosine $$d_1({\mathbf{v}}_i^{\left(f\right)},{\mathbf{v}}_j^{\left(f\right)})$$; and (bottom) Jaccard $$d_2({\mathbf{v}}_i^{\left(f\right)},{\mathbf{v}}_j^{\left(f\right)})$$. The points represent the test cases. On the left, lines connect points of constant $$\delta$$, and each color corresponds to points of constant $$\alpha$$. On the right, lines connect points of constant $$\alpha$$, and each color corresponds to points of constant $$\delta$$. The fractional order $${\alpha }_q\in [-0.5,1]$$, the width of the band $${\delta }_q\in [{10}^{-4},{10}^1]$$, and $$f_r\in [{10}^{-2},{10}^2]$$ Hz.

Figure 7

The 3-dim MDS locus for the FVSC-ISM, assessing the time domain-behavior, with the distances: (top) Arccosine $$d_1({\mathbf{v}}_i^{\left(t\right)},{\mathbf{v}}_j^{\left(t\right)})$$; and (bottom) Jaccard $$d_2({\mathbf{v}}_i^{\left(t\right)},{\mathbf{v}}_j^{\left(t\right)})$$. The points represent the test cases. On the left, lines connect points of constant $$\delta$$, and each color corresponds to points of constant $$\alpha$$. On the right, lines connect points of constant $$\alpha$$, and each color corresponds to points of constant $$\delta$$. The fractional order $${\alpha }_q\in [-0.2,6]$$, and the width of the band $${\delta }_q\in [{10}^{-4},{10}^1]$$.

Figure 8

The 3-dim MDS locus for the FVSC-ISM, assessing the frequency-domain behavior, with the distances: (top) Arccosine $$d_1({\mathbf{v}}_i^{\left(f\right)},{\mathbf{v}}_j^{\left(f\right)})$$; and (bottom) Jaccard $$d_2({\mathbf{v}}_i^{\left(f\right)},{\mathbf{v}}_j^{\left(f\right)})$$. The points represent the test cases. On the left, lines connect points of constant $$\delta$$, and each color corresponds to points of constant $$\alpha$$. On the right, lines connect points of constant $$\alpha$$, and each color corresponds to points of constant $$\delta$$. The fractional order $${\alpha }_q\in [-0.2,0.6]$$, the width of the band $${\delta }_q\in [{10}^{-4},{10}^1]$$, and $$f_r\in [{10}^{-2},{10}^2]$$ Hz.