Dynamic maximum entropy provides accurate approximation of structured population dynamics

Abstract

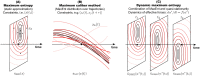
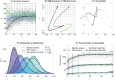
Realistic models of biological processes typically involve interacting components on multiple scales, driven by changing environment and inherent stochasticity. Such models are often analytically and numerically intractable. We revisit a dynamic maximum entropy method that combines a static maximum entropy with a quasi-stationary approximation. This allows us to reduce stochastic non-equilibrium dynamics expressed by the Fokker-Planck equation to a simpler low-dimensional deterministic dynamics, without the need to track microscopic details. Although the method has been previously applied to a few (rather complicated) applications in population genetics, our main goal here is to explain and to better understand how the method works. We demonstrate the usefulness of the method for two widely studied stochastic problems, highlighting its accuracy in capturing important macroscopic quantities even in rapidly changing non-stationary conditions. For the Ornstein-Uhlenbeck process, the method recovers the exact dynamics whilst for a stochastic island model with migration from other habitats, the approximation retains high macroscopic accuracy under a wide range of scenarios in a dynamic environment.

Fig 1. Variational methods ME and MC compared to DME.

(A) ME looks at a snapshot x of a process at a particular time and provides an approximation ${\overline{u}}_{\text{ME}}\left(\mathbf{x}\right)$ of the microscopic distribution, given knowledge of a few key macroscopic observables. (B) MC is analogous to ME, however, each data point represents a trajectory x(t). MC connects the microscopic distribution over possible trajectories with macroscopic constraints and approximates it by ${\overline{u}}_{\text{MC}}\left(x\left(t\right)\right)$. (C) DME is a quasi-stationary approximation of the stochastic dynamics, given by the FPE, which reduces the full problem to a low-dimensional dynamics. This reduction is a consequence of a ME ansatz; the approximation at each time ${\overline{u}}_{\text{DME}}\left(\mathit{\alpha }\left(t\right)\right)$ solves the ME problem (stationary form in the FPE), where the dynamics of the effective forces α are systematically derived from the FPE.

Fig 2. Numerical example of the OU process.

(A) Numerical simulations of the OU process with parameters β_∞ = 0.7, μ_∞ = 1, σ₀ = 0.1. We used three random initial conditions from a distribution $\mathcal{N}(x_0,{\sigma }_0)$ with μ₀ = x₀ = 1.2, 0.6, 0.1 and β₀ = 0.7, 0.5, 0.45. (B) Effective forces (μ*, β*) following dynamics in Eqs 31 and 32 corresponding to the same set of initial conditions as in panel A. (C) Histograms of x(t) at times t = 0.3, 1, 2, 5 (initial condition β₀ = 0.45, μ₀ = 0.1, σ₀ = 0.1 as in panel A) from the simulated data and approximated distributions in Eq 16 for the effective forces. The time points correspond to the diamonds of matching color in the panels A-B. Code in S1 Code.

Fig 3. Numerical example of the island model.

(A) Numerical simulations of stochastic population dynamics on a single island with immigration. Parameters are α₁ = {r, λ, m} = {0.1, 0.002, 3}. We used initial conditions, α_0,1 = {0.05, 0.005, 1} (black), α_0,2 = {0.15, 0.005, 5} (blue), and α_0,3 = {0.08, 0.001, 2} (green). (B) Corresponding dynamics of the effective forces projected to the (r, λ) space. (C) Irreversibility of the process: 2D projections of the trajectories between α₁ = {0.1, 0.002, 3} and α_0,1 = {0.05, 0.005, 1} and reversed are not the same. (D) Histograms of population sizes at t = 1, 5, 10, 40 with initial condition α_0,1 = {0.05, 0.005, 1} (black curves in panels A-B). The numerical solution of the corresponding FPE, the discrete transition matrix prediction, and the DME all show a close match. (E) The three observables n, log(n), and n²/2. Code in S1 Code.

Fig 4. Periodic changes in carrying capacity between 20 and 50.

The system starts from equilibrium with parameters {0.05, 0.005, 1} (as in Fig 3), then periodic shifts occur between {0.1, 0.0005, 3} and {0.1, 0.0002, 3} (blue, red, yellow). The equilibrium distribution of population size is shown as it changes in time (background colors). The black dashed line is the mean equilibrium population size, the black solid line shows the solution of the DME, whereas the white is the solution of the FPE. The error is measured by relative entropy, see the Eq 6.