Nucleation kinetics of calcium oxalate monohydrate as a function of pH, magnesium, and osteopontin concentration quantified with droplet microfluidics

Abstract

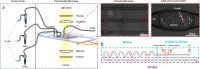
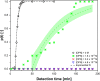
A droplet-based microfluidic platform is presented to study the nucleation kinetics of calcium oxalate monohydrate (COM), the most common constituent of kidney stones, while carefully monitoring the pseudo-polymorphic transitions. The precipitation kinetics of COM is studied as a function of supersaturation and pH as well as in the presence of inhibitors of stone formation, magnesium ions (Mg²⁺), and osteopontin (OPN). We rationalize the trends observed in the measured nucleation rates leveraging a solution chemistry model validated using isothermal solubility measurements. In equimolar calcium and oxalate ion concentrations with different buffer solutions, dramatically slower kinetics is observed at pH 6.0 compared to pHs 3.6 and 8.6. The addition of both Mg²⁺ and OPN to the solution slows down kinetics appreciably. Interestingly, complete nucleation inhibition is observed at significantly lower OPN, namely, 3.2 × 10^-8 M, than Mg²⁺ concentrations, 0.875 × 10^-4 M. The observed inhibition effect of OPN emphasizes the often-overlooked role of macromolecules on COM nucleation due to their low concentration presence in urine. Moreover, analysis of growth rates calculated from observed lag times suggests that inhibition in the presence of Mg²⁺ cannot be explained solely on altered supersaturation. The presented study highlights the potential of microfluidics in overcoming a major challenge in nephrolithiasis research, the overwhelming physiochemical complexity of urine.

FIG. 1.

Experimental setup and microfluidic platform: (a) Schematic of the experimental setup with insets showing polarized light microscopy images of droplets during induction time measurements. (b) Illustration of the droplet formation, the mixing, and the storage zones in the microfluidic platform.

FIG. 2.

The total dissolved calcium concentration in equilibrium for different pH values (a) and for different magnesium concentrations (panel b). The solid symbols are measured values with ICP-OES, and open symbols are the predicted values via our solution chemistry model, respectively. Calcium values represent the average of nine data points for each pH value and magnesium concentration. The regression statistics give a p-value of 0.08 for Fig. 2(b).

FIG. 3.

Microscopy image of the microfluidic chip (a) showing droplet generation, mixing, and storage zones. Time-lapse images of individual droplets captured under polarized light microscopy [(b)–(d)]. The calcium and oxalate ion concentrations in ultrapure water are equal, [Ca²⁺] = [C₂O₄²⁻] = 4.10 × 10⁻⁴ M, which corresponds to S = 2.74 predicted by the solution chemistry model.

FIG. 4.

The cumulative induction time probability, p(t), as a function of the detection time, t, for different added Ca²⁺ concentrations in ultrapure water fitted with the exponential function with delay time [Eq. (1)]. The numbers of used droplets are 107, 112, 129, 102, and 103 for concentrations of 1.35 × 10⁻⁴, 2.05 × 10⁻⁴, 2.75 × 10⁻⁴, 4.10 × 10⁻⁴, and 5.50 × 10⁻⁴ M, respectively. The ratio of added molar concentration of Ca²⁺ and C₂O₄²⁻ ions is the same for all experiments [Ca²⁺]/[C₂O₄²⁻] = 1 for all solutions. The calculated initial free Ca²⁺ and C₂O₄²⁻ ion concentrations, their activity coefficient, and the initial supersaturation of COM in the droplets are given in Table II.

FIG. 5.

The cumulative induction time probability, p(t), curves for different pH values fitted with the single exponential with delay time [Eq. (1)]. The numbers of used droplets are 118, 105, and 124 for pH values of 3.6, 6.0, and 8.6, respectively. The composition of the buffer solutions for pH values of 3.6, 6.0, and 8.6 are shown in Table I. The added equimolar Ca²⁺ and C₂O₄²⁻ concentration of 4.1 × 10⁻⁴ M is used in all experiments. The calculated initial free Ca²⁺ and C₂O₄²⁻ ion concentrations, their activity coefficient, and the initial supersaturation of COM in the droplets are given in Table III.

FIG. 6.

The cumulative induction time probability curves, p(t), at specific Mg²⁺ concentrations fitted with the single exponential with delay time [Eq. (1)]. The numbers of used droplets are 107, 106, 109, 113, 108, and 102 for concentrations of magnesium: 0, 0.05 × 10⁻⁴, 0.5 × 10⁻⁴, 0.875 × 10⁻⁴, 1 × 10⁻⁴, and 1.25 × 10⁻⁴ M, respectively. The varying concentrations of Mg²⁺ ions are added to equimolar calcium and oxalate concentration of [Ca²⁺] = [C₂O₄²⁻]= 4.1 × 10⁻⁴ M. The calculated initial free Ca²⁺ and C₂O₄²⁻ ion concentrations, their activity coefficient, and the initial supersaturation of COM in the droplets are given in Table IV.

FIG. 7.

The cumulative induction time probability, p(t), curves at specific osteopontin concentrations fitted with the single exponential with delay time [Eq. (1)]. The numbers of used droplets is 107, 102, 111, and 105 for concentrations of osteopontin: 0, 1.6 × 10⁻⁸, 3.2 × 10⁻⁸, and 4.8 × 10⁻⁸ M, respectively. The Ca²⁺ and C₂O₄²⁻ concentrations are kept constant at 4.1 × 10⁻⁴ M.

FIG. 8.

Apparent nucleation rate, J, and the corresponding S value for all of the measured induction times of COM at different conditions plotted in the context of classic nucleation time, i.e., different calcium and oxalate ion concentrations in de-ionized water given in Fig. 4, different pH values given in Fig. 5, and magnesium ion concentrations given in Fig. 6. Only the induction time data for different calcium and oxalate ion concentrations (green data points) in de-ionized water are fitted to Eq. (3). The dotted line is the fit with the parameters A = 4.05 × 10⁸ m⁻³ s⁻¹ (1.83 × 10⁷ to 8.96 × 10⁹) and B = 0.47 (−0.80 to 1.73) and gray shaded area is the 95% confidence interval.

FIG. 9.

Analysis of measured growth rates of COM calculated from delay times in p(t) curves for different calcium and oxalate ion concentrations given in Fig. 4 (green dots) and magnesium ion concentrations given in Fig. 6 (red squares).

FIG. 10.

Characterization of the crystal structure of the formed crystals under various conditions. (a) Raman spectra of collected droplets removed from the oil phase (red); COM crystals suspended in ultrapure water (green), COM Powder from supplier (magenta), and ultrapure water (black). (b) XRD spectra of dried crystals from droplets (red), COM powder from supplier (black), COM reference (dark green), COD reference (orange), and COT reference (purple).