Uncovering Non-random Binary Patterns Within Sequences of Intrinsically Disordered Proteins
- PMID: 34863777
- PMCID: PMC10178624
- DOI: 10.1016/j.jmb.2021.167373
Uncovering Non-random Binary Patterns Within Sequences of Intrinsically Disordered Proteins
Abstract
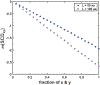
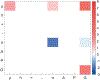
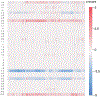
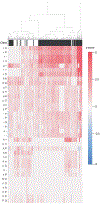
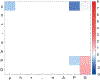
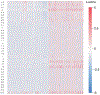
Sequence-ensemble relationships of intrinsically disordered proteins (IDPs) are governed by binary patterns such as the linear clustering or mixing of specific residues or residue types with respect to one another. To enable the discovery of potentially important, shared patterns across sequence families, we describe a computational method referred to as NARDINI for Non-random Arrangement of Residues in Disordered Regions Inferred using Numerical Intermixing. This work was partially motivated by the observation that parameters that are currently in use for describing different binary patterns are not interoperable across IDPs of different amino acid compositions and lengths. In NARDINI, we generate an ensemble of scrambled sequences to set up a composition-specific null model for the patterning parameters of interest. We then compute a series of pattern-specific z-scores to quantify how each pattern deviates from a null model for the IDP of interest. The z-scores help in identifying putative non-random linear sequence patterns within an IDP. We demonstrate the use of NARDINI derived z-scores by identifying sequence patterns in three well-studied IDP systems. We also demonstrate how NARDINI can be deployed to study archetypal IDPs across homologs and orthologs. Overall, NARDINI is likely to aid in designing novel IDPs with a view toward engineering new sequence-function relationships or uncovering cryptic ones. We further propose that the z-scores introduced here are likely to be useful for theoretical and computational descriptions of sequence-ensemble relationships across IDPs of different compositions and lengths.
Keywords: CIDER; NARDINI; binary patterns; intrinsically disordered proteins/regions.
Copyright © 2021 The Author(s). Published by Elsevier Ltd.. All rights reserved.
Conflict of interest statement
Declaration of interests The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.
Figures



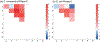

References
-
- Ward JJ, Sodhi JS, McGuffin LJ, Buxton BF, Jones DT, (2004). Prediction and functional analysis of native disorder in proteins from the three kingdoms of life. J Mol Biol, 337, 635–645. - PubMed
-
- Peng Z, Mizianty MJ, Kurgan L, (2014). Genome-scale prediction of proteins with long intrinsically disordered regions. Proteins: Structure, Function, and Bioinformatics, 82, 145–158. - PubMed
Publication types
MeSH terms
Substances
Grants and funding
LinkOut - more resources
Full Text Sources

