Second sound in the crossover from the Bose-Einstein condensate to the Bardeen-Cooper-Schrieffer superfluid
- PMID: 34873169
- PMCID: PMC8648831
- DOI: 10.1038/s41467-021-27149-z
Second sound in the crossover from the Bose-Einstein condensate to the Bardeen-Cooper-Schrieffer superfluid
Abstract
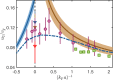
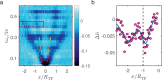
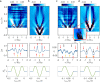
Second sound is an entropy wave which propagates in the superfluid component of a quantum liquid. Because it is an entropy wave, it probes the thermodynamic properties of the quantum liquid. Here, we study second sound propagation for a large range of interaction strengths within the crossover between a Bose-Einstein condensate (BEC) and the Bardeen-Cooper-Schrieffer (BCS) superfluid, extending previous work at unitarity. In particular, we investigate the strongly-interacting regime where currently theoretical predictions only exist in terms of an interpolation in the crossover. Working with a quantum gas of ultracold fermionic 6Li atoms with tunable interactions, we show that the second sound speed varies only slightly in the crossover regime. By varying the excitation procedure, we gain deeper insight on sound propagation. We compare our measurement results with classical-field simulations, which help with the interpretation of our experiments.
© 2021. The Author(s).
Conflict of interest statement
The authors declare no competing interests.
Figures

Similar articles
-
Excitation Spectrum and Superfluid Gap of an Ultracold Fermi Gas.Phys Rev Lett. 2022 Mar 11;128(10):100401. doi: 10.1103/PhysRevLett.128.100401. Phys Rev Lett. 2022. PMID: 35333076
-
Emergence of a molecular Bose-Einstein condensate from a Fermi gas.Nature. 2003 Dec 4;426(6966):537-40. doi: 10.1038/nature02199. Epub 2003 Nov 26. Nature. 2003. PMID: 14647340
-
Josephson effect in fermionic superfluids across the BEC-BCS crossover.Science. 2015 Dec 18;350(6267):1505-8. doi: 10.1126/science.aac9725. Epub 2015 Dec 17. Science. 2015. PMID: 26680193
-
Collective excitations in two-component ultracold quantum matter.J Phys Condens Matter. 2025 Jun 12;37(25). doi: 10.1088/1361-648X/addc28. J Phys Condens Matter. 2025. PMID: 40403756 Review.
-
Microscopic dynamics and Bose-Einstein condensation in liquid helium.J Phys Condens Matter. 2023 Jan 24;35(8). doi: 10.1088/1361-648X/acaba3. J Phys Condens Matter. 2023. PMID: 36595229 Review.
References
-
- Donnelly, R. J. The two-fluid theory and second sound in liquid helium. Physics Today, 34–39 (October 2009).
-
- Pitaevskii, L. & Stringari, S. Second Sound in Ultracold Atomic Gases. Universal Themes of Bose-Einstein Condensation (pp. 322–347) (Cambridge University Press, 2015).
-
- Peshkov VP. Second sound in helium II. Sov. Phys. JETP. 1960;11:580.
-
- Griffin A. New light on the intriguing history of superfluidity in liquid 4He. J. Phys.: Condens. Matter. 2009;21:164220. - PubMed
LinkOut - more resources
Full Text Sources

